Create a MATLAB function:

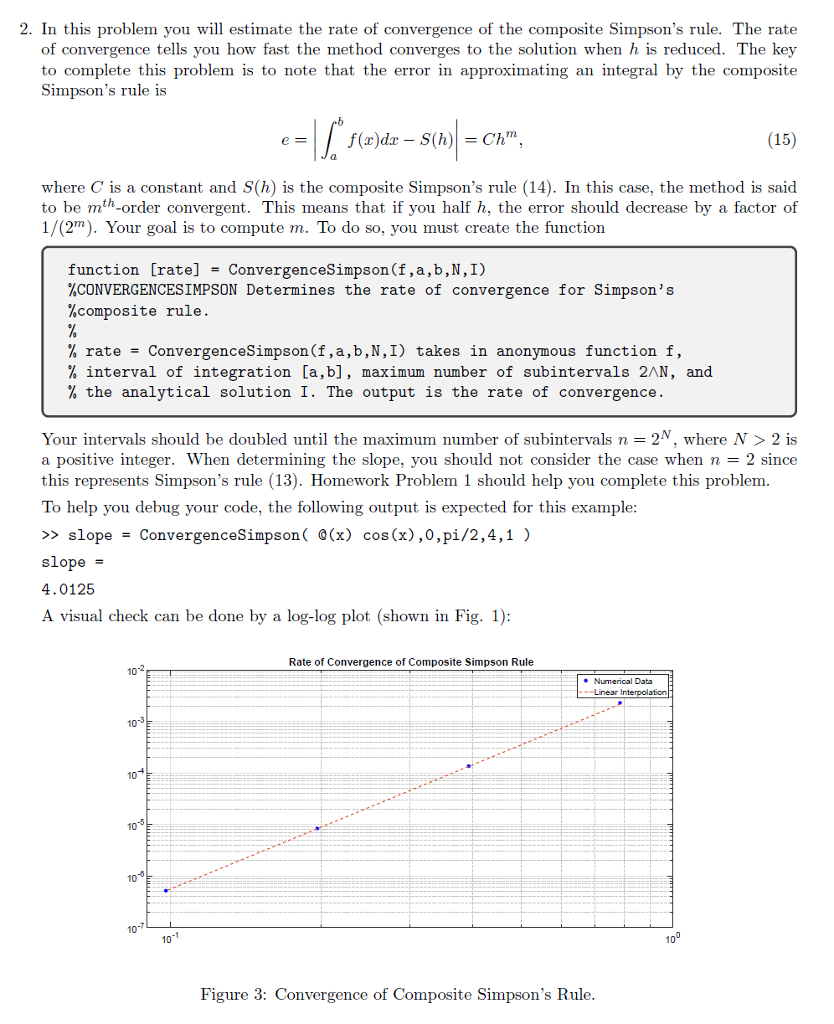
Homework Problem 3: Numerical Integration with Simpson's Rule In this exercise, you will create a function to compute definite integrals using Simpson's rule and the com posite Simpson's rule. For an interval of integration [a, b, Simpson's rule approximates the definite integral of f(r) by (13) Divide [a, into n equal subintervals of length h to obtain the composite Simpson's rule n/2-1 rn (14) where xj = a+jh and h = (b-a). Note that n need to be even 1. Write a function called Simpson to evaluate the definite integral of a given function f(x) on an interval [a, b. You must follow the pseudo-code: function [I,h] - Simpson (f,a,b,tol) %SIMPSON Compute definite integral of function using composite Simpson rule % 1 Simpson (f,a,b,tol) takes as inputs anonymous function f, the limits % of the interval of integration [a,b] and tolerance tol. Output is the % definite integral 1 and subinterval length h Initialization Set n = 2 and use Eq. (13) to compute a first approximation 101d Repeat Set 101d = 1 Double n and compute I with Eq. (14) Stop when tol You should run a few tests with Simpson to make sure it works properly. For exarnple, if f(z) = cos(2), then cos(a)dx - sins sin(0) = 1 In this case, your function should return >> [t-simp ,h] = Simpson (0(x) cos (x) ,0,pi/2 ,10-3) t-simp = 1.0000 0.1963 >> t-simp-1 ans 8.2955e-06 % error Homework Problem 3: Numerical Integration with Simpson's Rule In this exercise, you will create a function to compute definite integrals using Simpson's rule and the com posite Simpson's rule. For an interval of integration [a, b, Simpson's rule approximates the definite integral of f(r) by (13) Divide [a, into n equal subintervals of length h to obtain the composite Simpson's rule n/2-1 rn (14) where xj = a+jh and h = (b-a). Note that n need to be even 1. Write a function called Simpson to evaluate the definite integral of a given function f(x) on an interval [a, b. You must follow the pseudo-code: function [I,h] - Simpson (f,a,b,tol) %SIMPSON Compute definite integral of function using composite Simpson rule % 1 Simpson (f,a,b,tol) takes as inputs anonymous function f, the limits % of the interval of integration [a,b] and tolerance tol. Output is the % definite integral 1 and subinterval length h Initialization Set n = 2 and use Eq. (13) to compute a first approximation 101d Repeat Set 101d = 1 Double n and compute I with Eq. (14) Stop when tol You should run a few tests with Simpson to make sure it works properly. For exarnple, if f(z) = cos(2), then cos(a)dx - sins sin(0) = 1 In this case, your function should return >> [t-simp ,h] = Simpson (0(x) cos (x) ,0,pi/2 ,10-3) t-simp = 1.0000 0.1963 >> t-simp-1 ans 8.2955e-06 % error