Create a Turing machine that when started anywhere on the tape will halt if and only if there is a 0 somewhere on the tape. You won't be able to test this one in JFLAP, since it only lets you enter a single input string as the starting configuration of the tape. For this problem, the tape can start with 0s and 1s scattered anywhere on the tape - they do not have to be contiguous. Any permutation of 0s, 1s and blanks is a possible starting configuration.

(Please answer the question in the same format as the example, please use JFLAP for drawing, please do not handwrite or copy, thank you!)

Example

Create a Turing machine that computes the function f(x) = 2x + 3, where x is a positive integer represented in unary. The Turing machine starts with the input already on the tape and the read/write head positioned over the leftmost symbol of the input, as in the examples in the textbook.

Example Answer

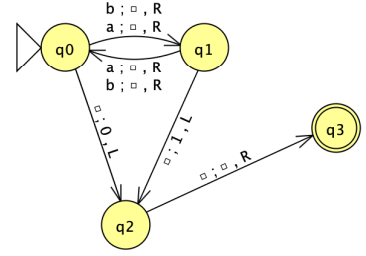
states: {q0,q1,q2,q3}

input alphabet: {a,b}

tape alphabet: {0,1,a,b,}

blank symbol:

initial state: q0

final states: {q3}

transitions:

(q2,) = (q3,,R)

(q0,b) = (q1,,R)

(q1,b) = (q0,,R)

(q0,) = (q2,0,L)

(q0,a) = (q1,,R)

(q1,a) = (q0,,R)

(q1,) = (q2,1,L)

use JFLAPuse JFLAPuse JFLAP

same formatsame formatsame format

no handwrite no handwrite no handwrite

If you copy, I will directly give you a negative-rating

b; -, R a; -, R D 90 91 a;,R b; -, R 0;0,1 l'Ila 93 0;O,R 42