Question: Create a user-defined MatLab function that implements the Gauss elimination method called Gauss_alt. The input arguments would matrix [a] and [b] from linear algebra ([a]*[x]=[b])
Create a user-defined MatLab function that implements the Gauss elimination method called Gauss_alt. The input arguments would matrix [a] and [b] from linear algebra ([a]*[x]=[b]) and the output [x]. If the input argument [b] is a row vector, the function should be able to transform it to a column vector. Use the augmented matrix for [a|b] for all operations in the function. Define the number of rows (R) and columns (C) using the size function in MatLab. For the elimination phase use two for-end loops, one inside the other, and a single expression in them (something=something). For the back substitution phase define the vector [x] outside the forend loop as a zero vector. Define the last value of [x] outside the for-end loop. Use one single expression inside the for-end loop (something=something). Solve the following set of equations by hand (explain the steps you are following):
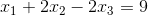
![Gauss_alt. The input arguments would matrix [a] and [b] from linear algebra](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/09/66f45718a4514_11266f4571852569.jpg)
![([a]*[x]=[b]) and the output [x]. If the input argument [b] is a](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/09/66f4571947ae0_11266f45718d6ce4.jpg)
Use the function Gauss_alt to validate your hand-calculated solution
11 + 2.02 - 2.63 9 2.01 +3.02 + 13 = 23 3.01 + 2.02 4.03 11 11 + 2.02 - 2.63 9 2.01 +3.02 + 13 = 23 3.01 + 2.02 4.03 11
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


