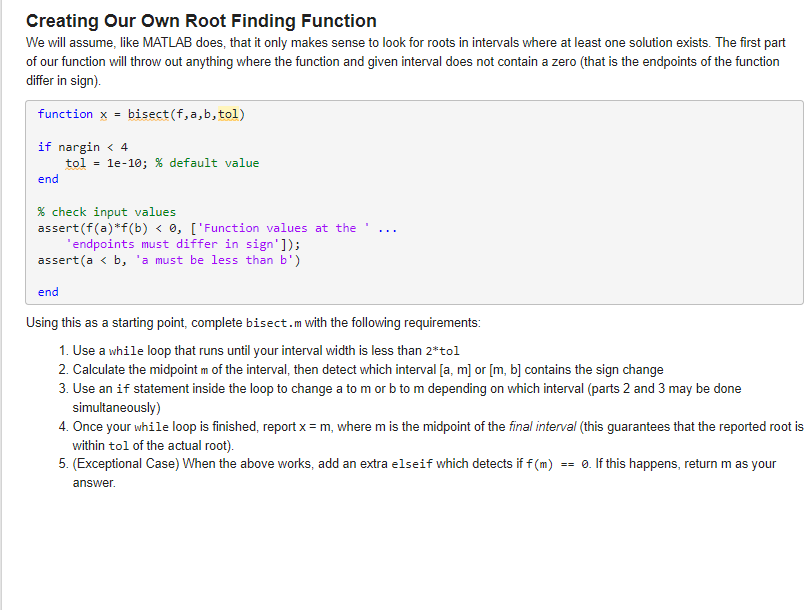
Question: Creating Our Own Root Finding Function We will assume, like MATLAB does, that it only makes sense to look for roots in intervals where at
Creating Our Own Root Finding Function
We will assume, like MATLAB does, that it only makes sense to look for roots in intervals where at least one solution exists. The first part
of our function will throw out anything where the function and given interval does not contain a zero that is the endpoints of the function
differ in sign
function x bisectf abtol
if nargin
tol e; default value
end
check input values
assertfafbFunction values at the
'endpoints must differ in sign';
asserta b 'a must be less than b
end
Using this as a starting point, complete bisect. with the following requirements:
Use a while loop that runs until your interval width is less than tol
Calculate the midpoint of the interval, then detect which interval or contains the sign change
Use an if statement inside the loop to change a to or to depending on which interval parts and may be done
simultaneously
Once your while loop is finished, report where is the midpoint of the final interval this guarantees that the reported root is
within tol of the actual root
Exceptional Case When the above works, add an extra elseif which detects if If this happens, return as your
answer.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


