Cryptography and Codes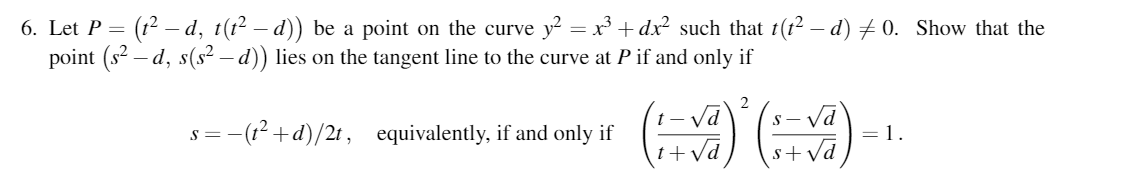

6. Let P = (t d, t(t d)) be a point on the curve y = x + dx such that t(t - d) 0. Show that the point (sd, s(s-d)) lies on the tangent line to the curve at P if and only if s=-(t+d)/2t, equivalently, if and only if 2 d =1. t+d