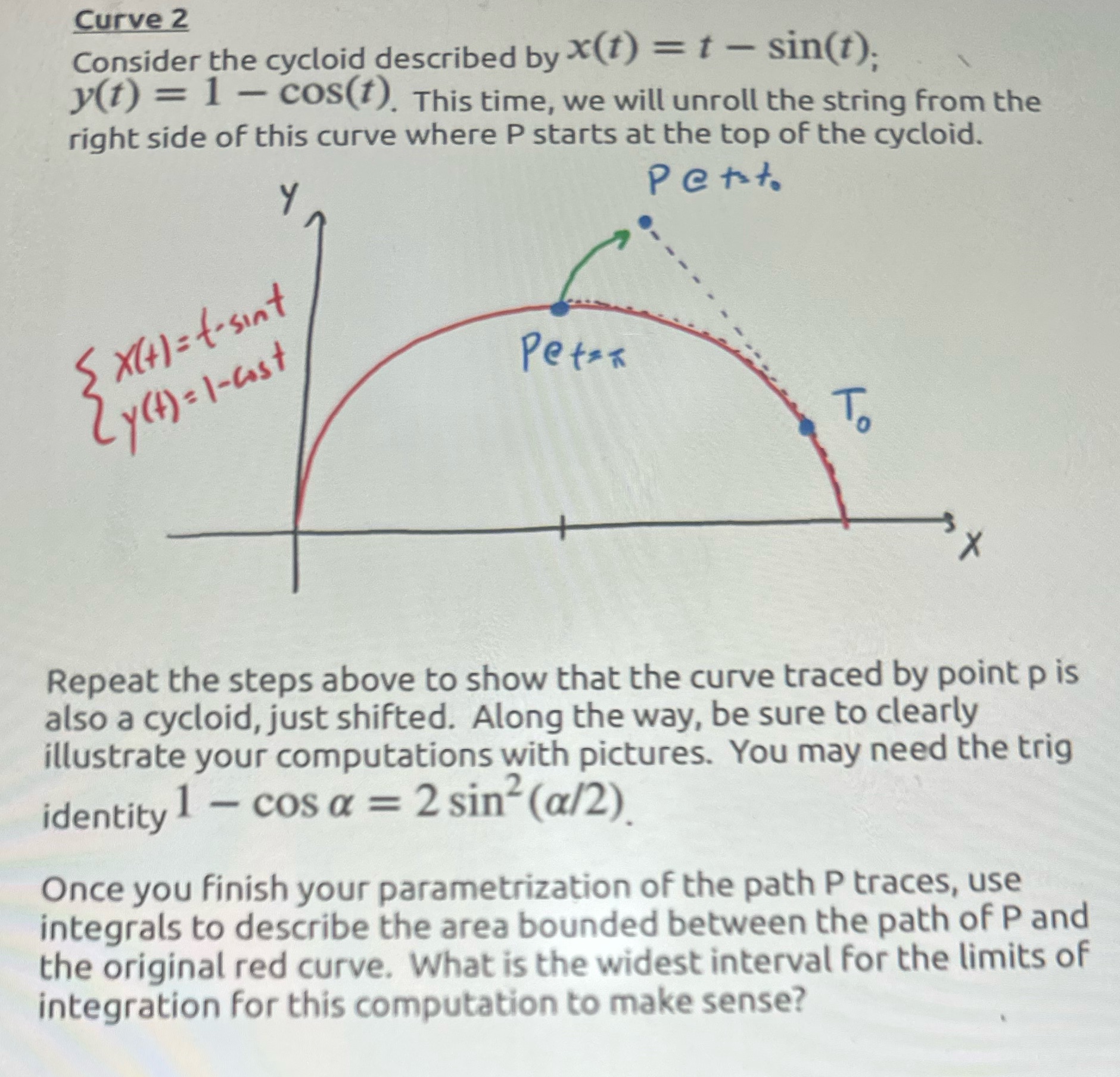
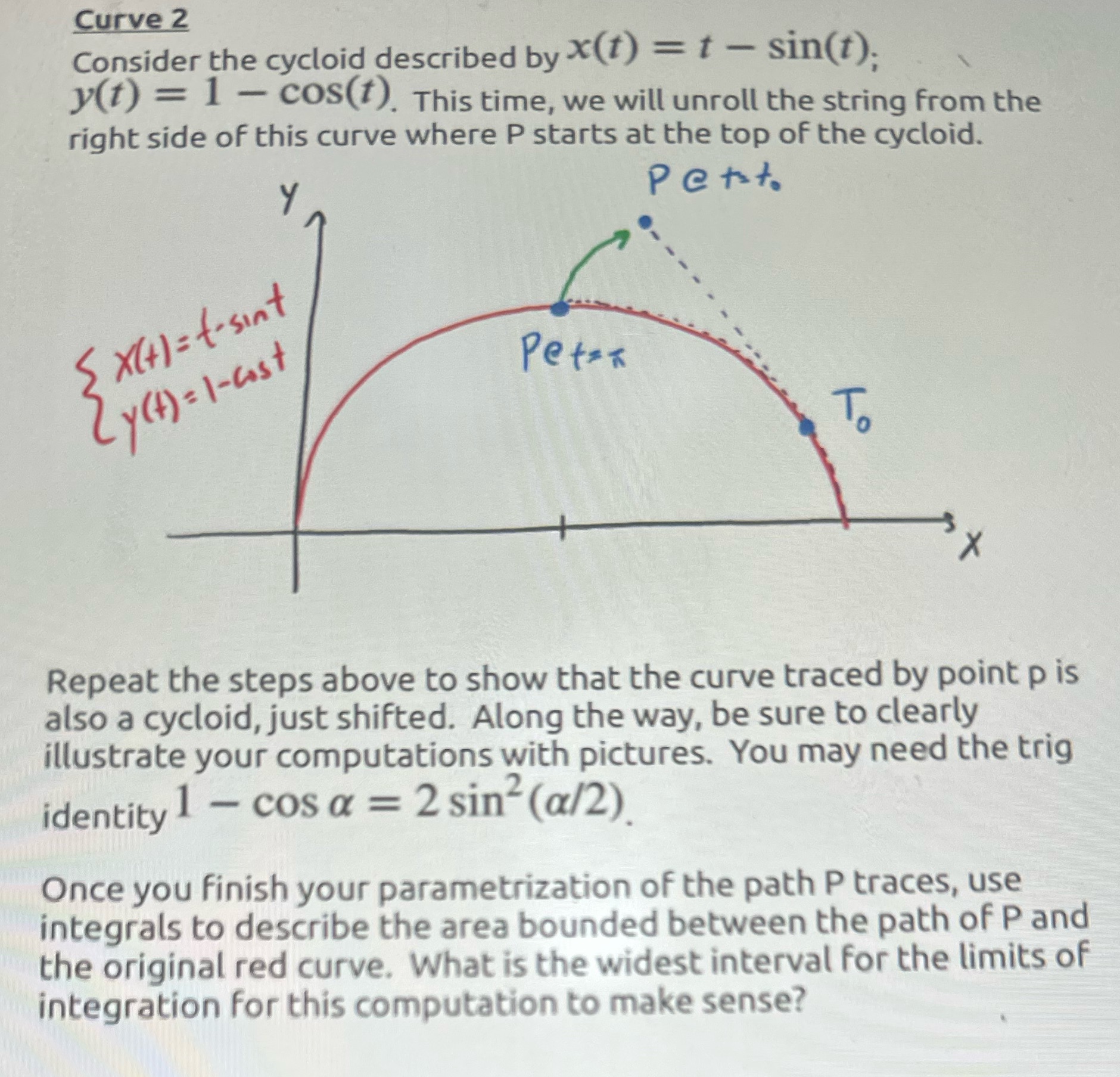
Curve 2 Consider the cycloid described by X(t) = t - sin(t); y(t) = 1 - cos(t). This time, we will unroll the string from the right side of this curve where P starts at the top of the cycloid. petit. 5 X (+1 = t-sint Petsx 2 y ( + ) = 1-cost Repeat the steps above to show that the curve traced by point p is also a cycloid, just shifted. Along the way, be sure to clearly illustrate your computations with pictures. You may need the trig identity 1 - cos a = 2 sin?(a/2). Once you finish your parametrization of the path P traces, use integrals to describe the area bounded between the path of P and the original red curve. What is the widest interval for the limits of integration for this computation to make sense