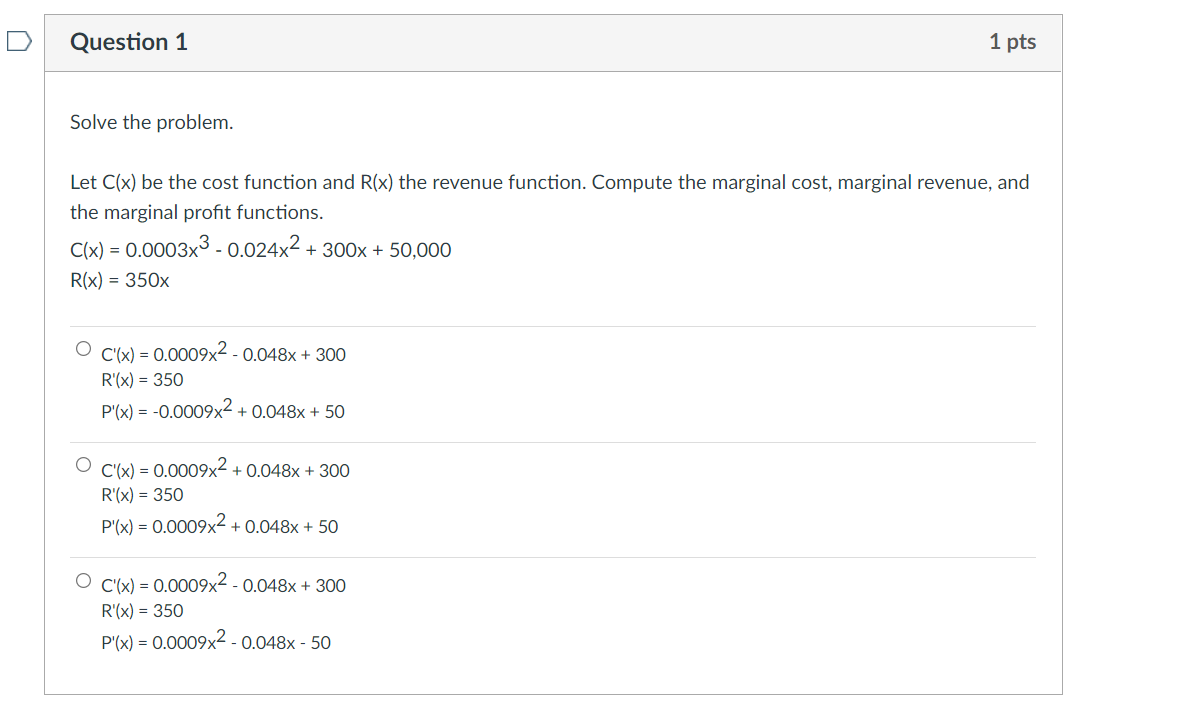
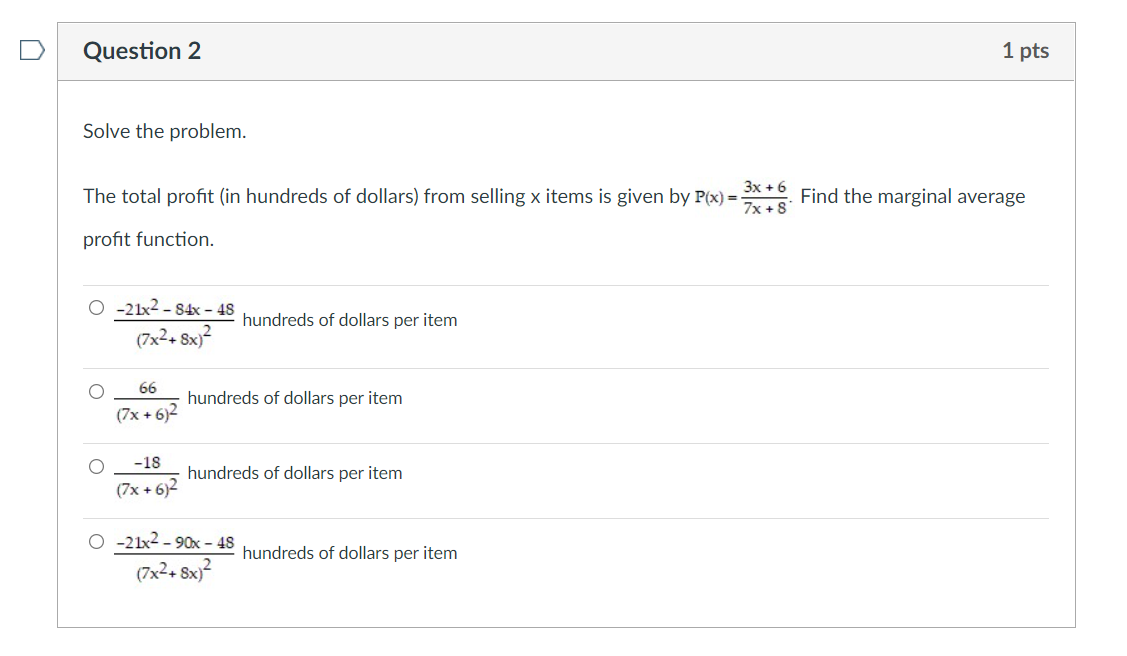
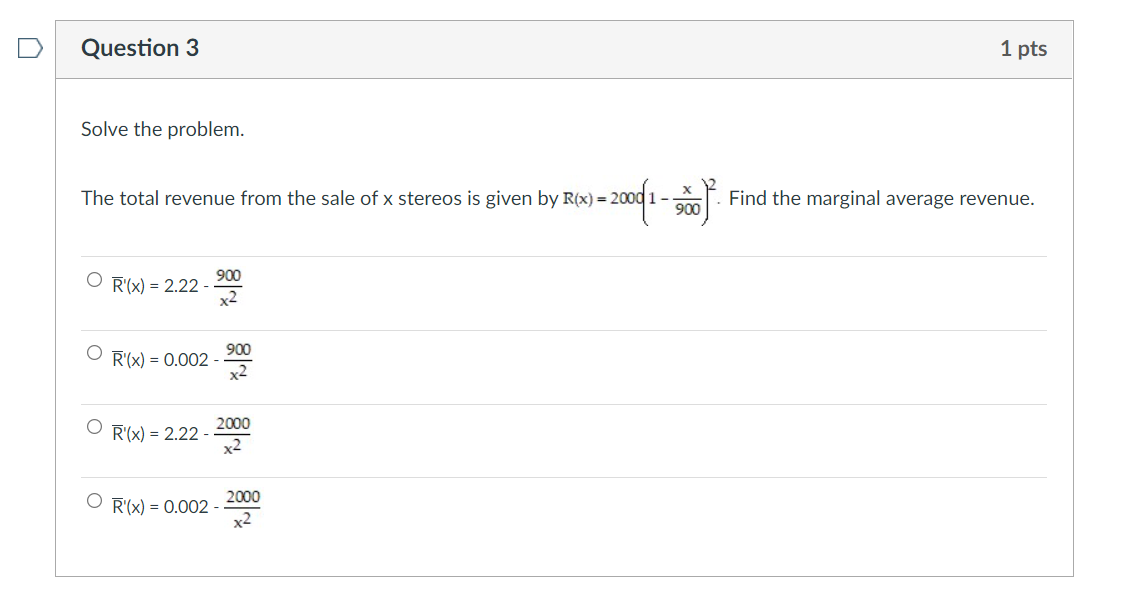
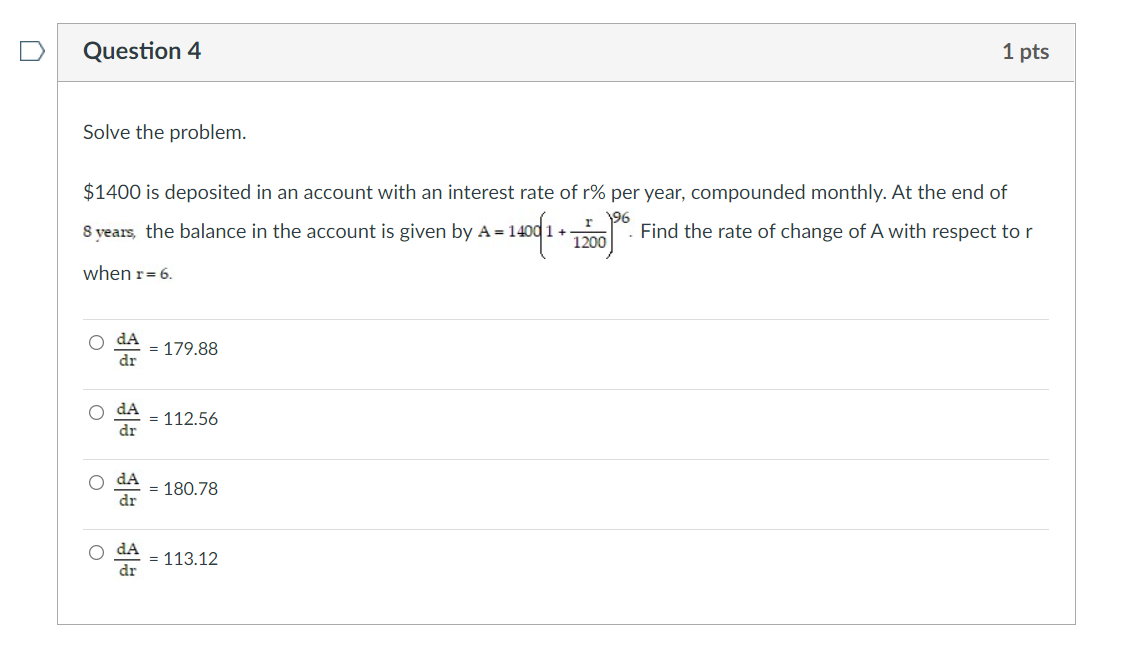
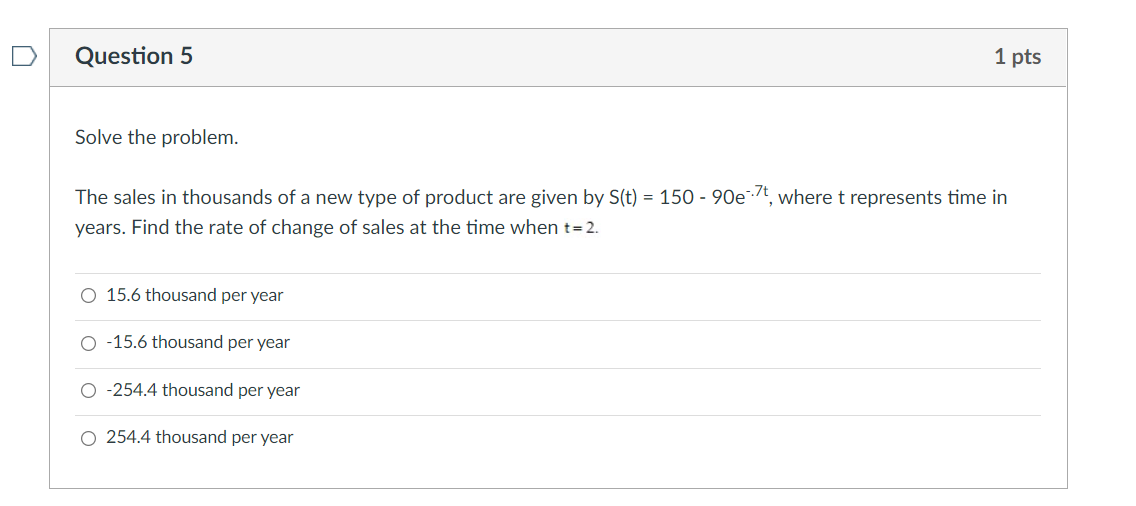
D Question 1 1 pts Solve the problem. Let C(x) be the cost function and R(x) the revenue function. Compute the marginal cost, marginal revenue, and the marginal profit functions. C(x) = 0.0003x3 - 0.024x2 + 300x + 50,000 R(x) = 350x . C'(x) = 0.0009x2 - 0.048x + 300 R'(x) = 350 P'(x) = -0.0009x2 + 0.048x + 50 . C'(x) = 0.0009x2 + 0.048x + 300 R'(x) = 350 P'(x) = 0.0009x2 + 0.048x + 50 . C'(x) = 0.0009x2 - 0.048x + 300 R'(x) = 350 P'(x) = 0.0009x2 - 0.048x - 50Question 2 Solve the problem. The total prot (in hundreds of dollars) from selling x items is given by Pm- prot function. 0 w hundreds of dollars per item (7x2+8x) O hundreds of dollars per item (7): +6)2 0 '18 hundreds of dollars per item (7): +6)2 0 -21x?- - 9cm - 4s hundreds of dollars per item (7x2+ 8x12 3x+6 7x+8' Find the marginal average D Question 3 1 pts Solve the problem. The total revenue from the sale of x stereos is given by R(x) = 2000 1 - -* 900 Find the marginal average revenue. O R'(x) = 2.22 - 900 x2 O R'(x) = 0.002 900 x2 O R'(x) = 2.22 2000 x2 O R'(x) = 0.002 - 2000 x2D Question 4 1 pts Solve the problem. $1400 is deposited in an account with an interest rate of r% per year, compounded monthly. At the end of 8 years, the balance in the account is given by A = 1400 1 + 1 6 1200 Find the rate of change of A with respect to r when r= 6. O dA = 179.88 dr O dA = 112.56 dr O dA dr = 180.78 O dA = 113.12 drQuestion 5 1 pts Solve the problem. The sales in thousands of a new type of product are given by S(t} = 150 - 90e'3t, where t represents time in years. Find the rate of change of sales at the time when t=2. O 15.6 thousand per year 0 -15.6 thousand per year 0 -254.4 thousand per year 0 254.4 thousand per year