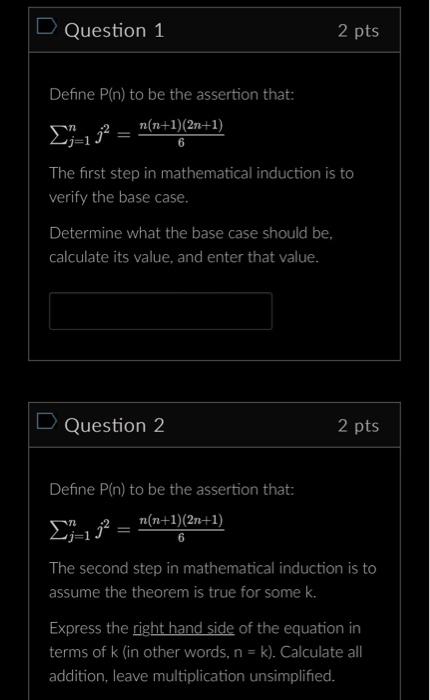
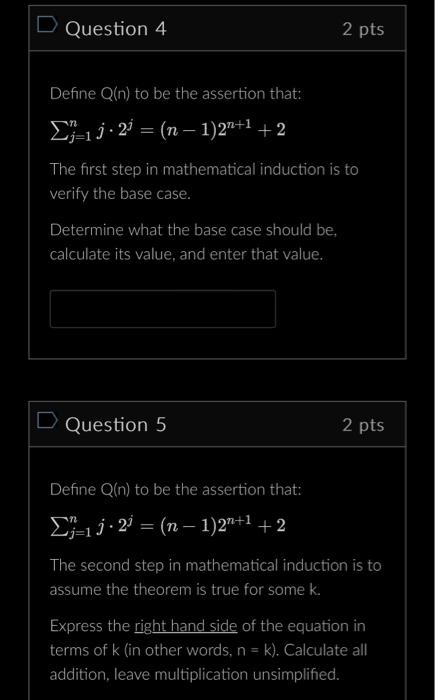
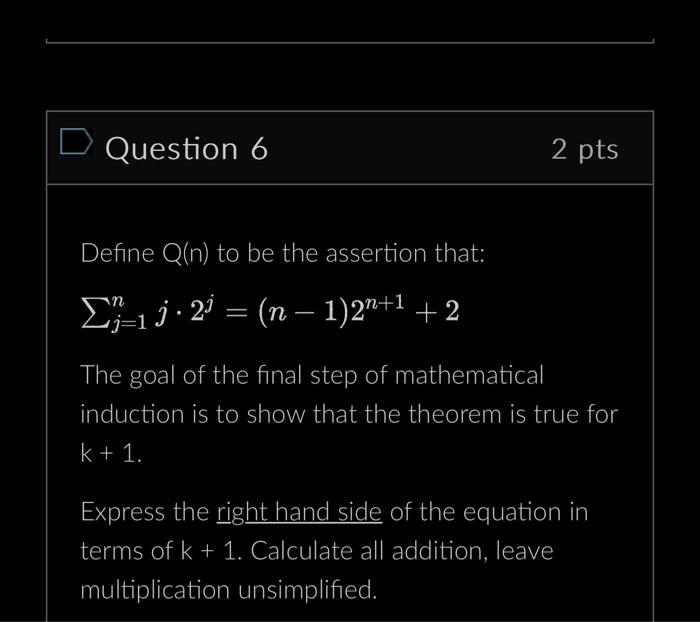
D Question 1 Define P(n) to be the assertion that: n(n+1) (2n+1) The first step in mathematical induction is to verify the base case. Determine what the base case should be. calculate its value, and enter that value. 2 pts D Question 2 2 pts Define P(n) to be the assertion that: -1 = n(n+1)(2n+1) 6 The second step in mathematical induction is to assume the theorem is true for some k. Express the right hand side of the equation in terms of k (in other words, n = k). Calculate all addition, leave multiplication unsimplified. D Question 3 Define P(n) to be the assertion that: n(n+1)(2n+1) 6 2 pts 132 The goal of the final step of mathematical induction is to show that the theorem is true for k+ 1. = Express the right hand side of the equation in terms of k + 1. Calculate all addition, leave multiplication unsimplified. D Question 4 Define Q(n) to be the assertion that: 1.2=(n-1) 2+1 +2 The first step in mathematical induction is to verify the base case. Determine what the base case should be, calculate its value, and enter that value. 2 pts D Question 5 2 pts Define Q(n) to be the assertion that: 1.2=(n-1)2+1 +2 The second step in mathematical induction is to assume the theorem is true for some k. Express the right hand side of the equation in terms of k (in other words, n= k). Calculate all addition, leave multiplication unsimplified. D Question 6 Define Q(n) to be the assertion that: 1 j 2 = (n 1)2n+1 +2 2 pts The goal of the final step of mathematical induction is to show that the theorem is true for k + 1. Express the right hand side of the equation in terms of k + 1. Calculate all addition, leave multiplication unsimplified.