DECISION PROBLEM 3: Managing Constraints Reminder: A single constraint in a system can impact the entire output as sub-processes sit idle, waiting for work. Identifying and reducing (even eliminating) a single constraint can have a dramatic improvement on performance and profitability. To match the three styles of window frames Olde World produces - the Abbot, the Berkeley, and the Cheshire - the company also produces the same three styles of door frames. These are fabricated at four different stations - W, X, Y and Z. They utilize a batch process that is quite efficient resulting in setup times that are negligible. The process sequence below shows the prices, weekly demand, and processing times for each of the three door styles. The costs for raw materials and any parts that are purchased from outside suppliers are per-unit consumption rates as shown in the inverted triangles. Additional information: ? There is no additional cost or penalty for not meeting the full demand. ? There is one worker at each station who is paid $20/hour and works a 40-hour week. ? Fixed costs for overhead are $10,000/week.

Based on the information above/below, answer the following questions: A. Which of the four processing stations has the highest aggregate workload, and therefore, is the bottleneck in the production of doors at Olde World? B. The company cannot always meet the demand for its doors, so the management team must make decisions about what quantities of each door it should produce to maximize profits. Because each of the three door styles has different costs and margins, Olde World has been prioritizing production by using a traditional method of accepting as much of the product with the highest margins up to the demand limit first, and then filling in the production plan with the next most profitable door and then the least profitable door. However, the Theory of Constraints (TOC) may suggest a way to improve profitability. i. How would profits be improved if a TOC/bottleneck-based method for scheduling were used to determine the product mix? Show calculations for both the traditional and TOC/bottleneck methods. ii. Explain why the TOC/bottleneck method is or is not superior for optimizing the profitability of the product mix.

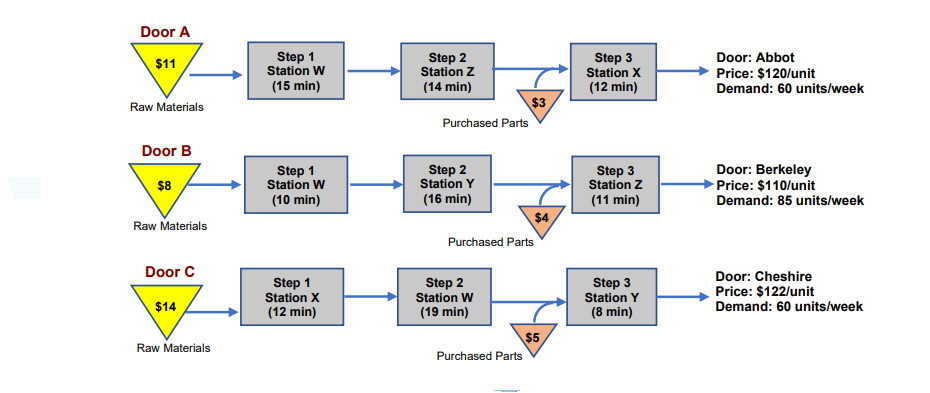
Door A $11 Step 1 Step 2 Step 3 Door: Abbot Station W Station Z Station X Price: $120/unit (15 min) (14 min) (12 min) Demand: 60 units/week Raw Materials $3 Purchased Parts Door B Step 1 Step 2 Step 3 Door: Berkeley $8 Station W Station Y Station Z Price: $110/unit (10 min) (16 min) (11 min) Demand: 85 units/week $4 Raw Materials Purchased Parts Door C Step 1 Step 2 Step 3 Door: Cheshire Station X Station W Station Y Price: $122/unit $14 (12 min) (19 min) (8 min) Demand: 60 units/week $5 Raw Materials Purchased Parts