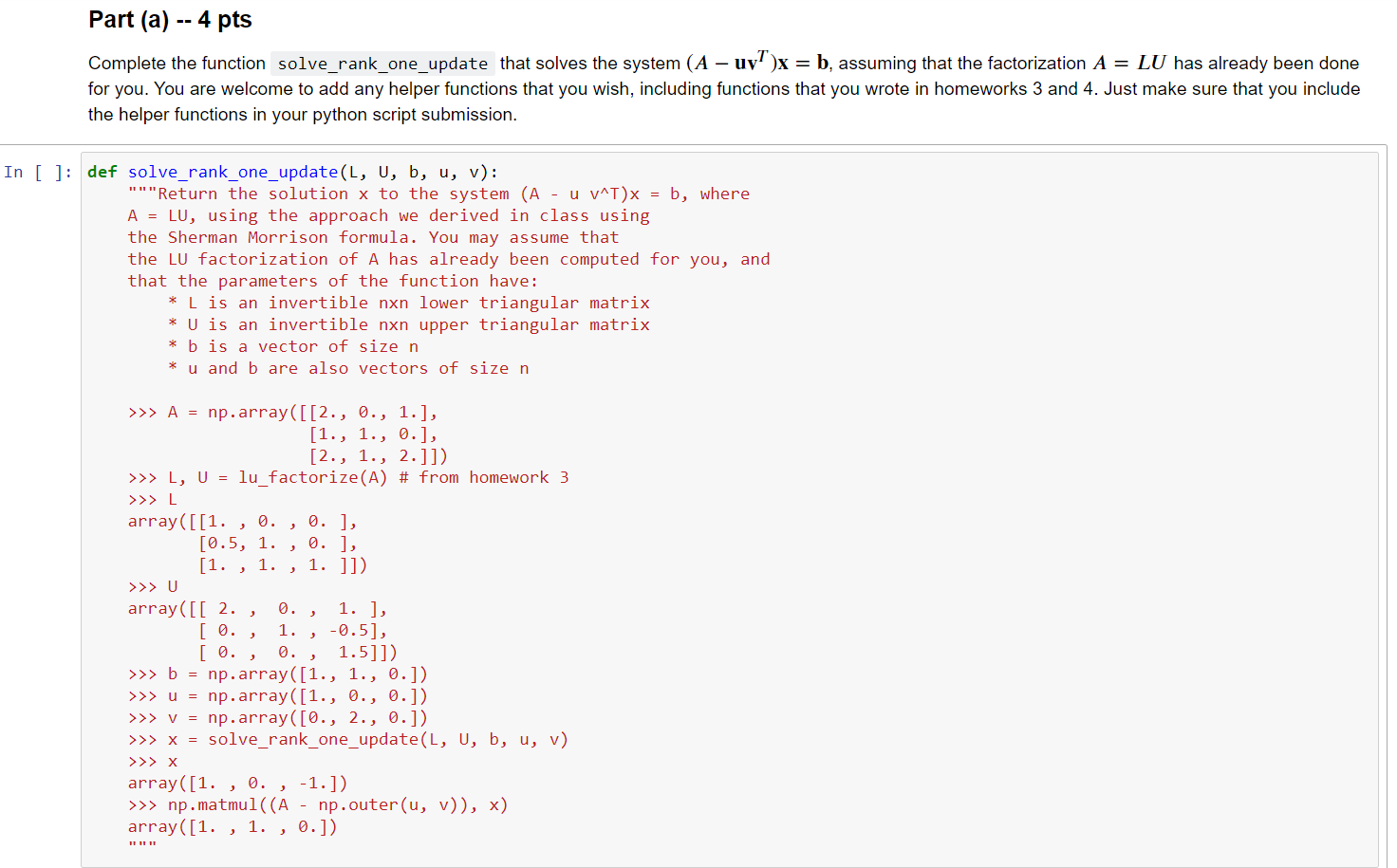
def solve_rank_one_update(L, U, b, u, v): """Return the solution x to the system (A - u v^T)x = b, where A = LU, using the approach we derived in class using the Sherman Morrison formula. You may assume that the LU factorization of A has already been computed for you, and that the parameters of the function have: * L is an invertible nxn lower triangular matrix * U is an invertible nxn upper triangular matrix * b is a vector of size n * u and b are also vectors of size n

>>> A = np.array([[2., 0., 1.], [1., 1., 0.], [2., 1., 2.]]) >>> L, U = lu_factorize(A) # from homework 3 >>> L array([[1. , 0. , 0. ], [0.5, 1. , 0. ], [1. , 1. , 1. ]]) >>> U array([[ 2. , 0. , 1. ], [ 0. , 1. , -0.5], [ 0. , 0. , 1.5]]) >>> b = np.array([1., 1., 0.]) >>> u = np.array([1., 0., 0.]) >>> v = np.array([0., 2., 0.]) >>> x = solve_rank_one_update(L, U, b, u, v) >>> x array([1. , 0. , -1.]) >>> np.matmul((A - np.outer(u, v)), x) array([1. , 1. , 0.]) """

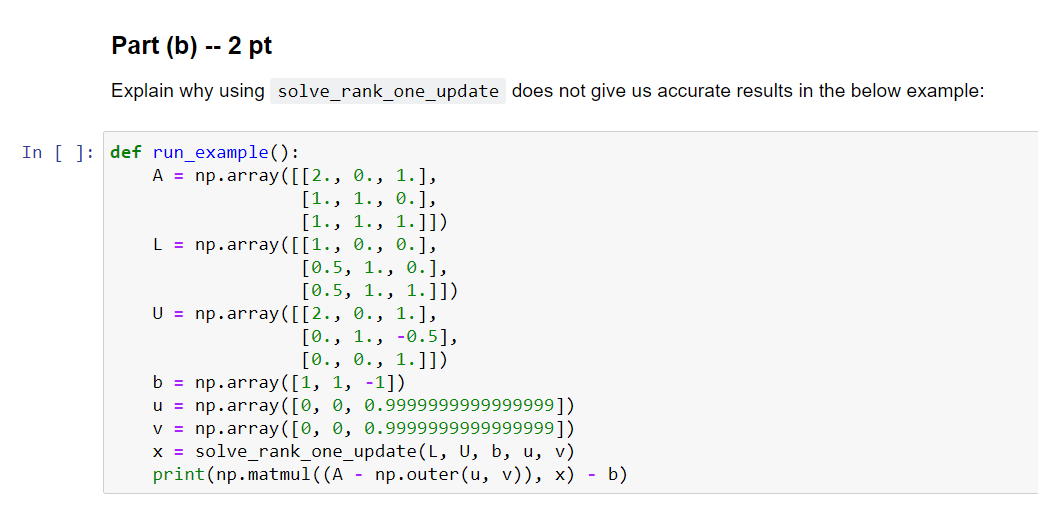
def run_example(): A = np.array([[2., 0., 1.], [1., 1., 0.], [1., 1., 1.]]) L = np.array([[1., 0., 0.], [0.5, 1., 0.], [0.5, 1., 1.]]) U = np.array([[2., 0., 1.], [0., 1., -0.5], [0., 0., 1.]]) b = np.array([1, 1, -1]) u = np.array([0, 0, 0.9999999999999999]) v = np.array([0, 0, 0.9999999999999999]) x = solve_rank_one_update(L, U, b, u, v) print(np.matmul((A - np.outer(u, v)), x) - b)

Part (a) - 4 pts Complete the function solve_rank_one_update that solves the system (A uyT)x = b, assuming that the factorization A = LU has already been done for you. You are welcome to add any helper functions that you wish, including functions that you wrote in homeworks 3 and 4. Just make sure that you include the helper functions in your python script submission. In [ ]: def solve_rank_one_update(L, U, b, u, v): """Return the solution x to the system (A - u v^)x = b, where A = LU, using the approach we derived in class using the Sherman Morrison formula. You may assume that the LU factorization of A has already been computed for you, and that the parameters of the function have: * L is an invertible nxn lower triangular matrix * U is an invertible nxn upper triangular matrix * b is a vector of size n u and b are also vectors of size n [1. , >>> A = np.array([[2., O., 1.), [1., 1., 0.], [2., 1., 2.]]) >>> L, U = lu_factorize(A) # from homework 3 >>> L array([[1. , 0., 0.] [0.5, 1. ,0. ], 1. , 1. ]]) >>> U array([[ 2. 0. 1. ], [ 0. , 1. -0.5], [ 0., 0., 1.5]]) >>> b = np.array([1., 1., 0.]) >>> u = np.array([1., O., 0.]) >>> v = np.array([0., 2., 0.]) >>> X = solve_rank_one_update(L, U, b, u, v) >>> X array([1. , 0, -1.]) >>> np.matmul((A - np.outer(u, v)), x) array([1. , 1., 0.]) Part (b) -- 2 pt Explain why using solve_rank_one_update does not give us accurate results in the below example: In [ ]: def run_example(): A = np.array([[2., 0., 1.), [1., 1., 0.], [1., 1., 1.]]) L = np.array([[1., O., 0.), [0.5, 1., 0.], [0.5, 1., 1.]]) U = np.array([[2., 9., 1.), [0., 1., -0.5], [0., 0., 1.]]) b = np.array([1, 1, -1]) u = np.array([0, 0, 0.9999999999999999]) V = np.array([0, 0, 0.9999999999999999]) x = solve_rank_one_update(L, U, b, u, v) print(np.matmul((A - np.outer(u, v)), x) - b) Part (c) -- 4 pt A rank 1 matrix has the form xywhere x and y are column vectors. Suppose A and B are non-sigular matrices. Show that A Bis rank 1 if and only if A-1 - B-1 is also rank 1. Include your solution in your pdf writeup. Hint: Use the Sherman-Morrison formula. This question is not supposed to be easy, so leave aside time to think