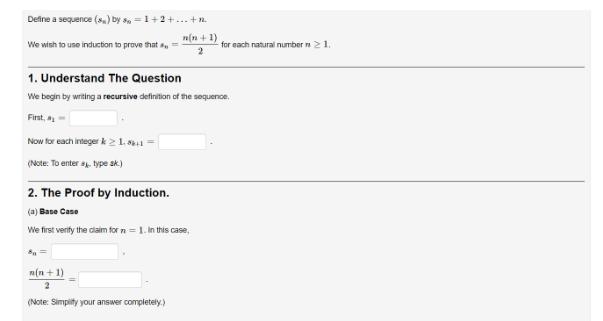
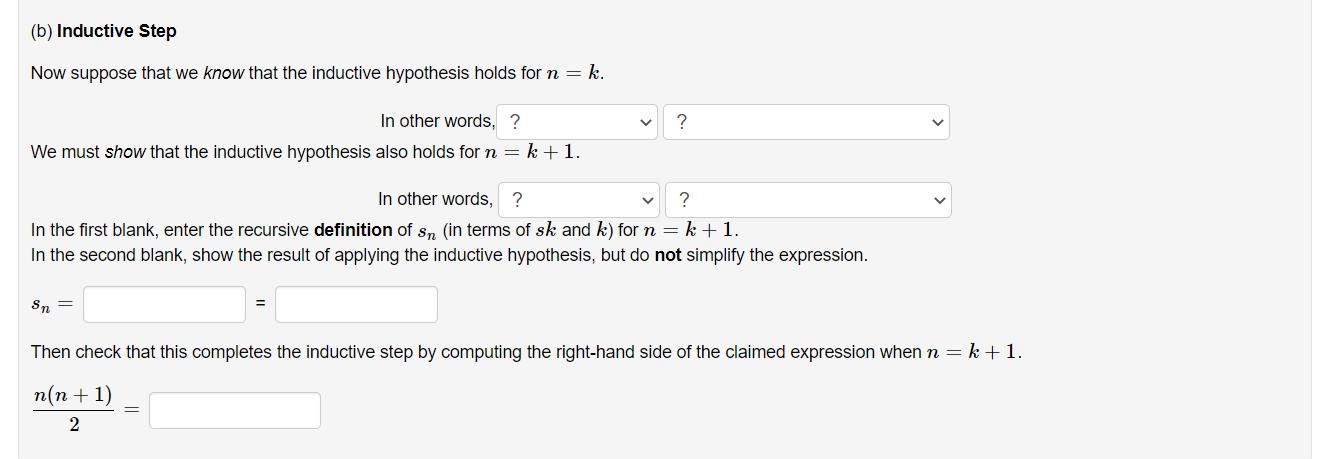
Define a sequence (s) by * = 1+2+...+ We wish to use induction to prove that = Now for each integer k21 (Note: To enter type ak.) n(n+1) 2 1. Understand The Question We begin by writing a recursive definition of the sequence. First, 2. The Proof by Induction. (a) Base Case We first verify the claim for n = 1. In this case, n(n+1) 2 (Note: Simplify your answer completely.) for each natural number n 1. (b) Inductive Step Now suppose that we know that the inductive hypothesis holds for n = k. In other words, ? We must show that the inductive hypothesis also holds for n = k + 1. In other words, ? ? In the first blank, enter the recursive definition of sn (in terms of sk and k) for n=k+1. In the second blank, show the result of applying the inductive hypothesis, but do not simplify the expression. Sn = ? V Then check that this completes the inductive step by computing the right-hand side of the claimed expression when n = k + 1. n(n+1) 2