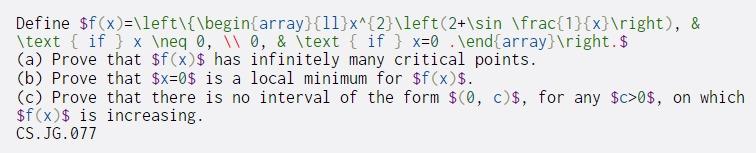
Define $f(x)=\left\{\begin{array}{11}x^{2}\left(2+\sin \frac{1}{x} ight), & \text { if } x eq 0, 0, & \text { if } x=0 .\end{array} ight. $ (a) Prove that $f(x)$ has infinitely many critical points. (b) Prove that $x=0$ is a local minimum for $f(x)$. (c) Prove that there is no interval of the form $(0, c)$, for any $c>0$, on which $f(x)$ is increasing. CS.JG.077