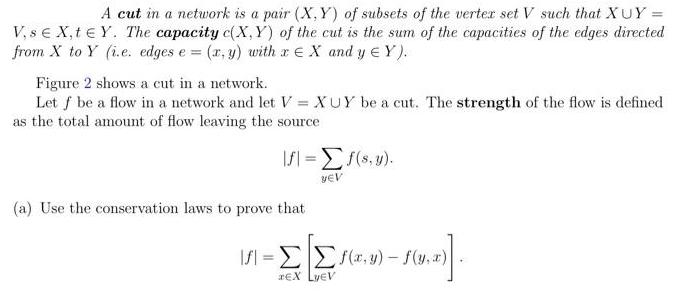
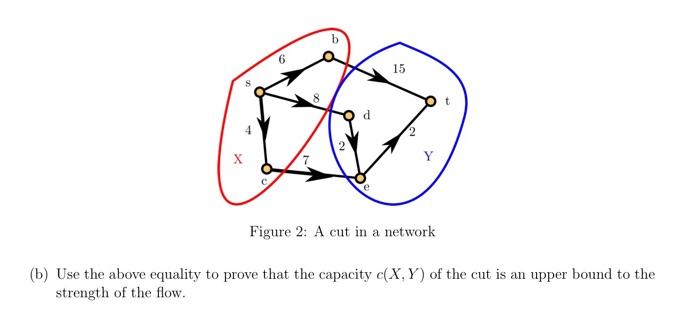
A cut in a network is a pair (X, Y) of subsets of the verter set V such that XUY = V, s e X, t Y. The capacity c(X, Y) of the cut is the sum of the capacities of the edges directed from X to Y (i.e. edges e = (r, y) with a E X and y E Y ). Figure 2 shows a cut in a network. Let f be a flow in a network and let V = XUY be a cut. The strength of the flow is defined as the total amount of flow leaving the source \S| =s, y). %3D VEV (a) Use the conservation laws to prove that =EE(,) - f(y,) rEX LyeV %3D 15 Figure 2: A cut in a network (b) Use the above equality to prove that the capacity c(X, Y) of the cut is an upper bound to the strength of the flow.