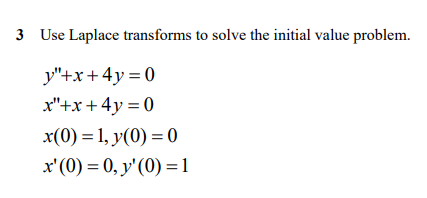
DEFINITION The Laplace Transform Given a function f(t) defined for all t0, the Laplace transform of f is the function F defined as follows: F(s) = {f(1)} = e" f(1) dt for all values of s for which the improper integral converges. Recall that an improper integral over an infinite interval is defined as a limit of integrals over bounded intervals; that is, fg(t) g(1) dt = lim bo, (1) g(t) dt. (2) 3 Use Laplace transforms to solve the initial value problem. y"+x+4y=0 x"+x+4y=0 x(0) = 1, y(0) = 0 x' (0) = 0, y' (0) = 1