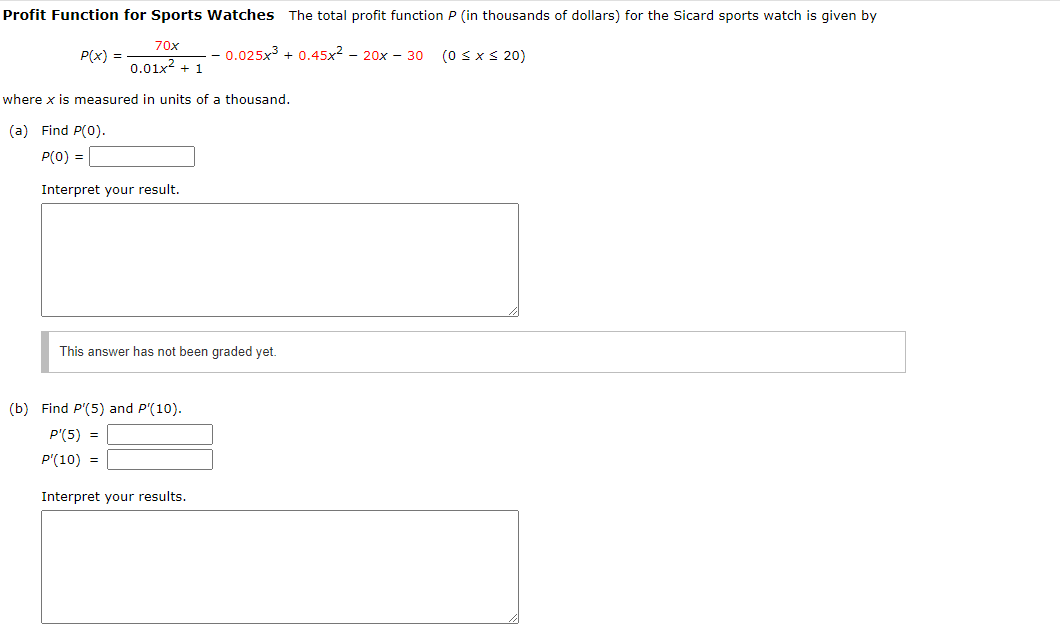
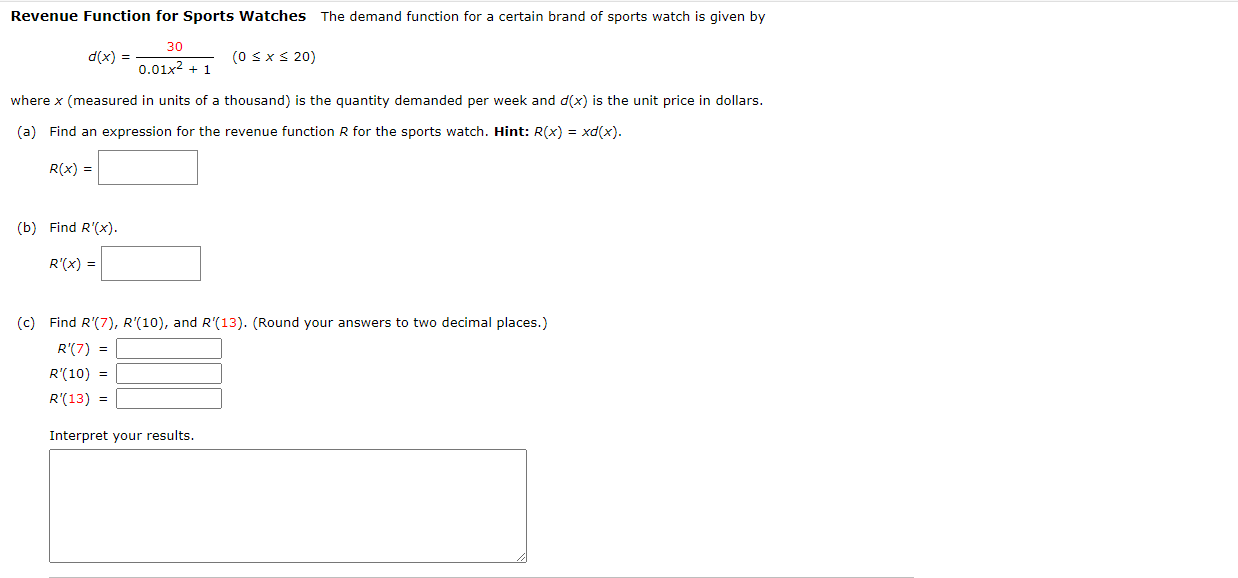
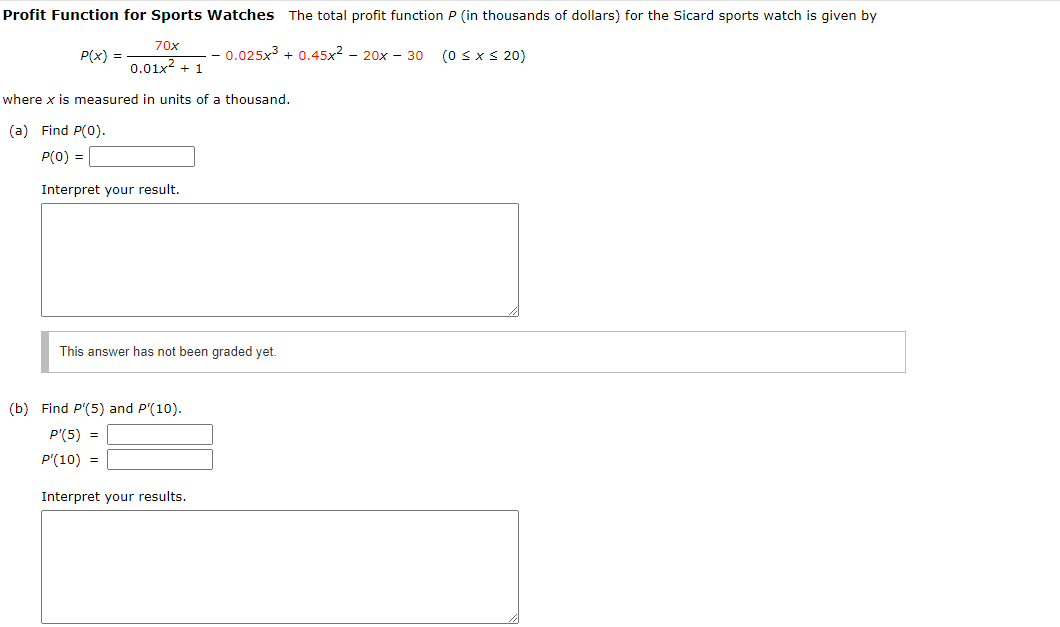
Demand Function for Sports Watches The demand function for the Sicard sports watch is given by 45 d[x) : 2 0.01)! + l (osxszo) where x (measured in units of a thousand) is the quantity demanded per week and (100 is the unit price in dollars. (a) Find d'(x}. x} = (b) Find the following values in dollars per thousand watches. {Round your answers to two decimal places.) 0"(5) = $ :l per thousand watches d'(].0) = $ :l per thousand watches d'(16) = $ :l per thousand watches Interpret the results. (Round your answers to two decimal places.) When the demand for watches is 5,000, the unit price For the watches is decreasing by $ :l per thousand watches. When the demand for watches is 10,000, the unit price for the watches is decreasing by $ :I per thousand watches. when the demand for watches is 16,000, the unit price for the watches is decreasing by $1; :I per thousand watches. Revenue Function for Sports Watches The demand function for a certain brand of sports watch is given by 30 d[x) = 2 0.011 + 1 {ogxszm where x {measured in units of a thousa nd} is the quantity demanded per week and d(x) is the unit price in dollars. {a} Find an expression For the revenue function R for the sports watch. Hint: R(x) = xd{x}. R(x) = (b) Find an). R'(x) : (c) Find R'(7), R'(10), and R'[13). (Round your answers to two decimal places.) m = :l 2m = E m = E Interpret your results. Profit Function for Sports Watches The total prot function P (in thousands of dollars} for the Sicard sports watch is given by 3'0x P{x} - 0.025,?3 : 0.45x2 20x 30 (0 Ex E 20] 0.:2-1x2 + 1 Where): is measured in units of a thousand. (3} Find pm). pm = :l Interpret your result. I This answer has not been graded yet. (b) Find i215) and p110}. pm = E m = E Interpret your results. Consider the following. 2 x}= x x+4 Find the derivative of the function. Find the slope m and an equation of the tangent line to the graph of the function fat the point (1, ). m = E Consider the following functions. g ( x) = x h(x) = vx+ X f ( x ) = x+7 Find the derivative of each function. g'(x) = h ' ( x ) = f' ( x) =