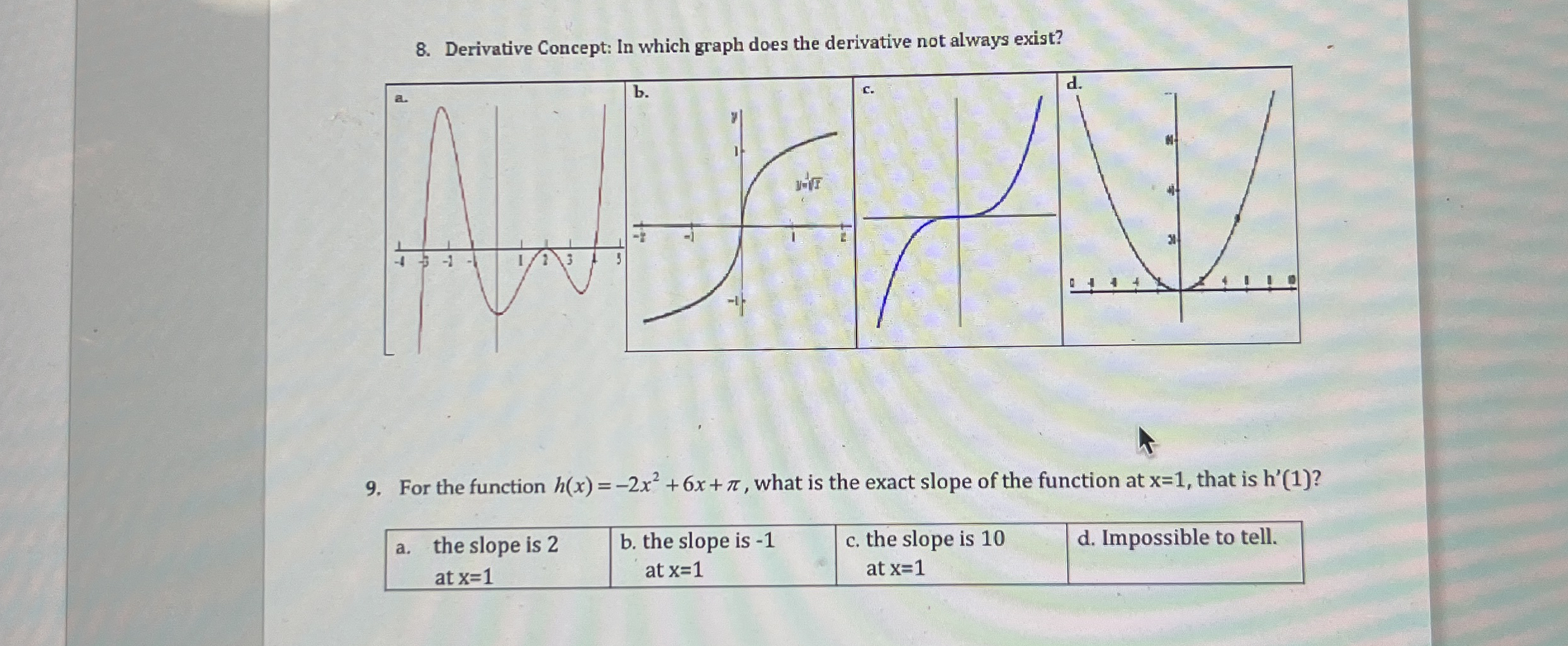
Question: Derivative Concept: In which graph does the derivative not always exist? For the function h ( x ) = - 2 x 2 + 6
Derivative Concept: In which graph does the derivative not always exist?
For the function what is the exact slope of the function at that is
a the slope is
b the slope is
c the slope is
d Impossible to tell. at at at
Derivative Concept: In which graph does the derivative not always exist?
For the function what is the exact slope of the function at that is
a the slope is
b the slope is
c the slope is
d Impossible to tell. at at at
Derivative Concept: In which graph does the derivative not always exist?
For the function what is the exact slope of the function at that is
a the slope is
b the slope is
c the slope is
d Impossible to tell. at at at
Derivative Concept: In which graph does the derivative not always exist?
For the function what is the exact slope of the function at that is
a the slope is
b the slope is
c the slope is
d Impossible to tell. at at at
Derivative Concept: In which graph does the derivative not always exist?
For the function what is the exact slope of the function at that is
a the slope is
b the slope is
c the slope is
d Impossible to tell. at at at
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


