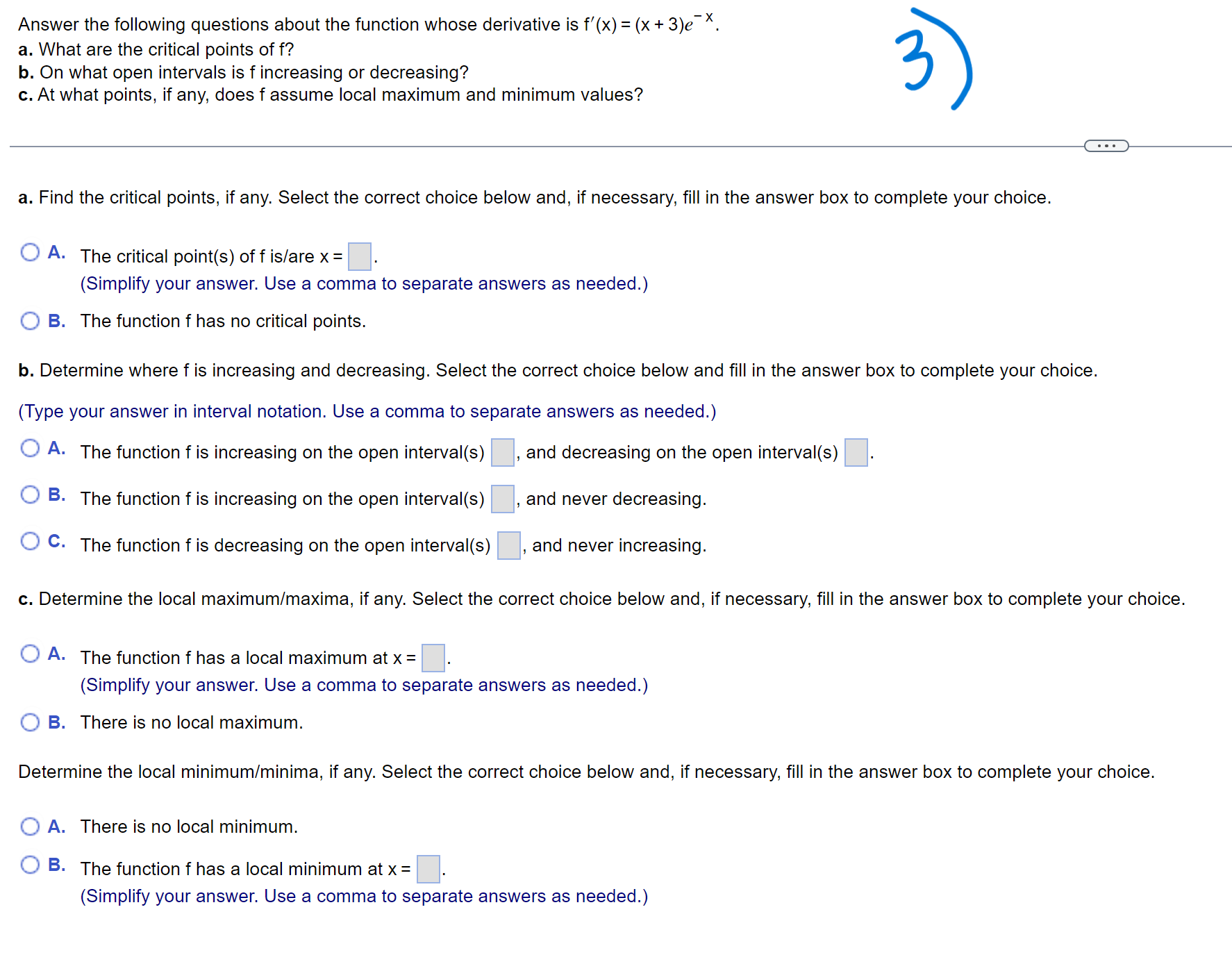
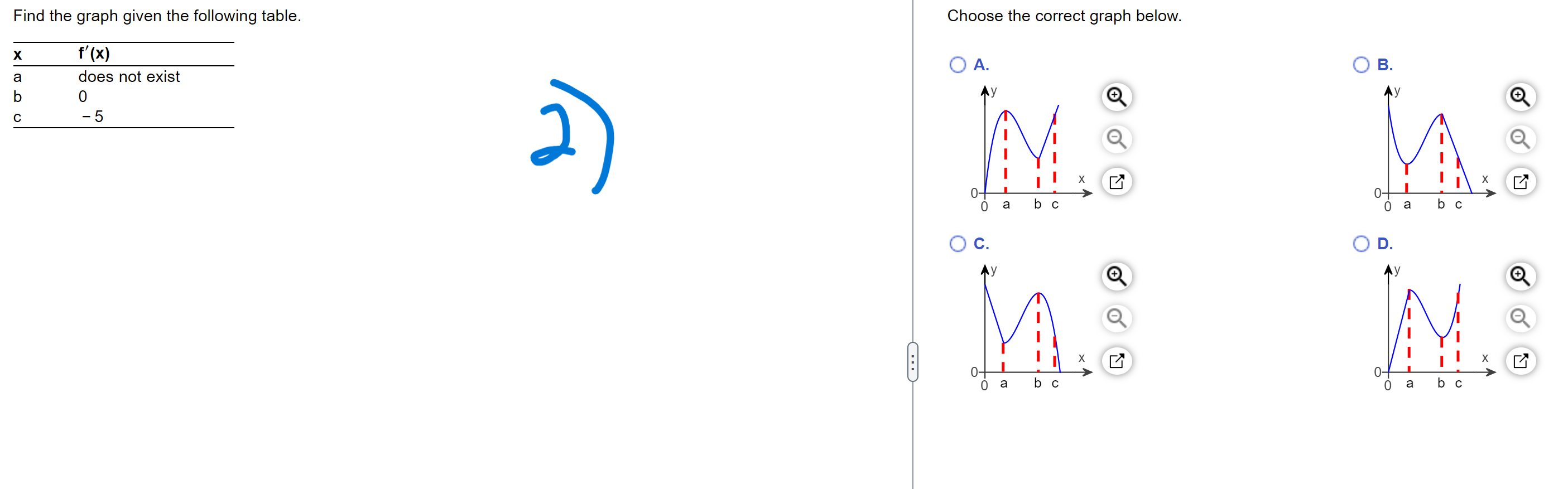
Does the function satisfy the hypotheses of the mean value theorem on the given interval? Give reasons for your answer. f(x) = y'x (7 x); [0,7] Choose the correct answer. \\ ' :- A. Yes, f(x) is continuous at every point in [0,7] and differentiable at every point in (0,7). B No, f(x) is continuous at every point in [0,7] but is not differentiable at every point in (0,7). 1_ _:- C. Yes, f(x) is continuous at every point in (0,7) and differentiable at every point in [0,7]. D No, f(x) is differentiable at every point in (0,7) but is not continuous at every point in [0,7]. Find the graph given the following table. Choose the correct graph below. f' ( x ) O A. O B. does not exist 0 - 5 X X 0 a b oa b c O c. OD. Ay X X 0 a b a b cAnswer the following questions about the function whose derivative is f'(x) = (x + 3)e_x. a. What are the critical points of f? b. On what open intervals is f increasing or decreasing? c. At what points, ifany, does f assume local maximum and minimum values? a. Find the critical points, if any. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. '3...\" A- The critical point(s) off is/are x= (Simplify your answer. Use a comma to separate answers as needed.) {In B. The function f has no critical points. b. Determine where f is increasing and decreasing. Select the correct choice below and fill in the answer box to complete your choice. (Type your answer in interval notation. Use a comma to separate answers as needed.) '1.\" A- The function f is increasing on the open interval(s) , and decreasing on the open interval(s) '3-'13' 3- The function f is increasing on the open interval(s) , and never decreasing. '1.\" C- The function f is decreasing on the open interval(s) , and never increasing. c. Determine the local maximum/maxima. if any. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A- The function f has a local maximum at x = (Simplify your answer. Use a comma to separate answers as needed.) '11\" B. There is no local maximum. Determine the local minimum/minima. if any. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. i] A. There is no local minimum. '3...\" 3- The function f has a local minimum at X: (Simplify your answer. Use a comma to separate answers as needed.) Find the indefinite integral 13 - X - 13 dx. X 3 13 1 4 13 X dx = X 3Two sides of a triangle are 8 and 11. Find the size of the angle 6 (in radians) formed by the sides that will maximize the area of the triangle. (.. The size of the angle 6 (in radians) that will maximize the area of the triangle is . 5 (Type an exact answer, using I as needed.) 5 Find the function with the derivative f'(x) = 362x whose graph passes through the point P [0 ]. L. The function passing through the point P is f(x) = D. i critical point = ) = - 3 "ce) : - e-R ( oct 3 ) + ex z - exx ( - 3 + 3 ) + e - 3 :. local minima at 2 = - 3 Local maxima does not exist