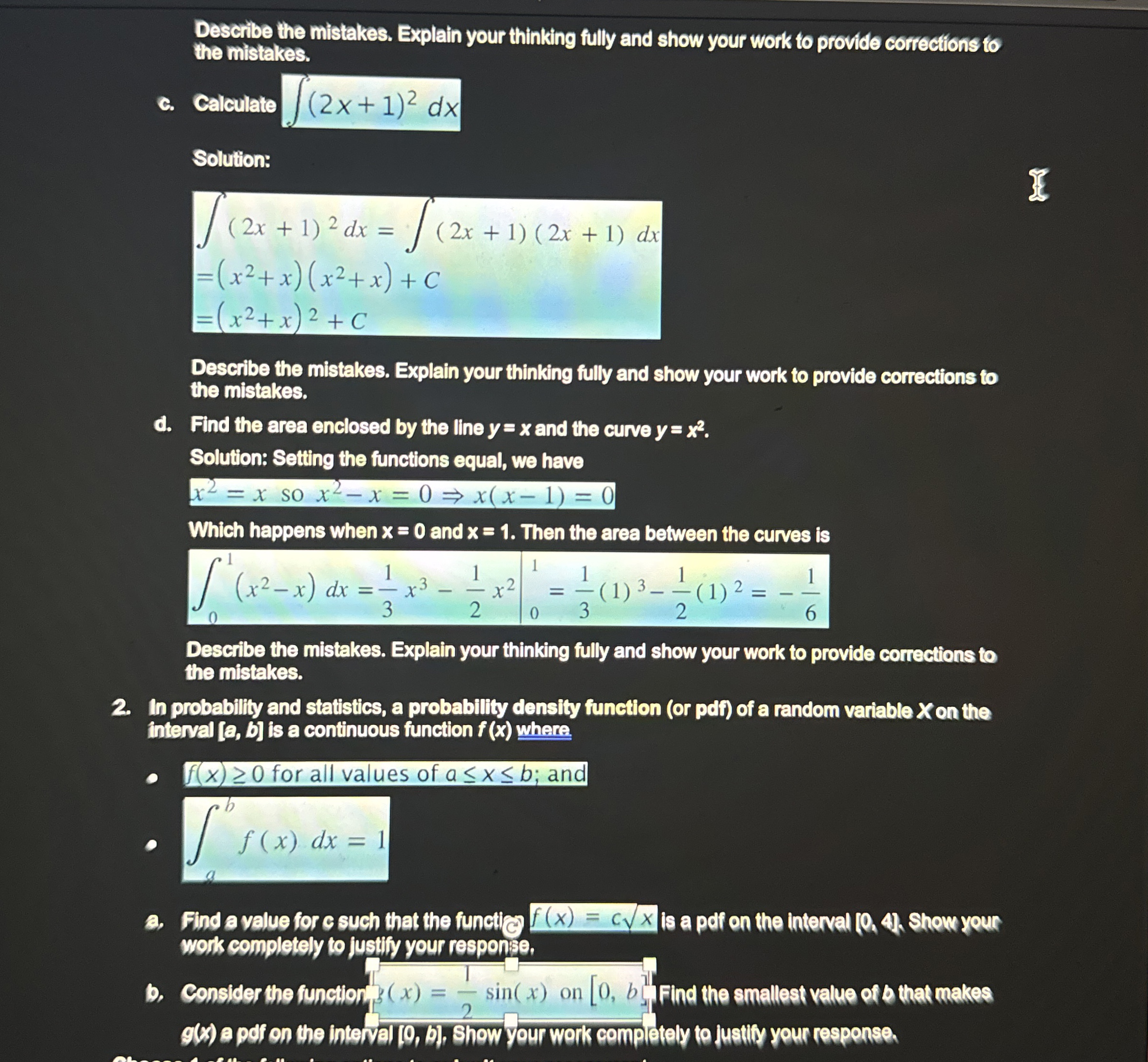
Question: Describe the mistakes. Explain your thinking fully and show your work to provide corrections to the mistakes. c . Calculate ( 2 x + 1
Describe the mistakes. Explain your thinking fully and show your work to provide corrections to the mistakes.
c Calculate
Solution:
Describe the mistakes. Explain your thinking fully and show your work to provide corrections to the mistakes.
d Find the area enclosed by the line and the curve
Solution: Setting the functions equal, we have
Which happens when and Then the area between the curves is
Describe the mistakes. Explain your thinking fully and show your work to provide corrections to the mistakes.
In probability and statistics, a probability density function or pdif of a random variable on the interval is a continuous function where
for all values of ; and
a Find a value for such that the functic is a pdf on the interval Show your work completely to justify your response.
b Consider the function on Find the smallest value of be that makes a pdf on the intervel b Show your werk completely to Justify your response.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


