Design a statistics structure that keeps a FIFO queue of integers, assisting operations ENQUEUE, DEUEUE, and FIND-MIN, every in O(1) amortized time. In other phrases, any series of m operations should take time O(m). You might also count on that, in any execution, all of the gadgets that get enqueued are distinct. (a) Describe your facts shape. Include clean invariants describing its key houses. Hint: Use an actual queue plus auxiliary statistics structure(s) for bookkeeping.

(b) Describe carefully, in words or pseudo-code, your ENQUEUE, DEQUEUE

and FIND-MIN approaches.

(c) Prove that your operations give the right solutions. Hint: You might also want to prove that their correctness follows out of your statistics shape invariants. In that case you must also sketch arguments for why the invariants maintain.

(d) Analyze the time complexity: the worst-case fee for each operation, and

the amortized fee of any sequence of m operations.

In a dynamic-set facts shape, the query FINGER-SEARCH(x, ok) is given a node x in the statistics structure and a key ok, and it have to return a node y inside the facts structure that consists of key okay. (You may additionally count on that the sort of node y in fact seems in the information structure.) The purpose is for FINGER-SEARCH to run faster when nodes x and y are close by within the information structure. (a) Write pseudocode for FINGER-SEARCH(x, ok) for pass lists. Assume all keys inside the bypass listing are distinct. Assume that the given node x is inside the stage-0 listing, and the operation must go back a node y that shops okay in the stage-zero listing. Your algorithm have to run in O(lg m) steps with excessive possibility, in whichrank(x.Key) ? rank(okay. Here, rank(ok) refers to the rank (index) of a key okay within the sorted order of the dynamic set (when the system is invoked). "High opportunity" here is with respect to m; greater precisely, for any fine integer ?, your algorithm need to run in O(lg m) time with possibility at least 1 ? 1/ma . (The steady implicit in this O may depend upon ?.) Analyze your algorithm cautiously. In writing your code, you could expect that the implementation of bypass lists shops each a ?? at the the front of every stage in addition to a +? because the closing detail on every stage. Another question on a dynamic set is RANK-SEARCH(x, r): given a node x inside the statistics shape and effective integer r, go back a node y in the statistics shape that incorporates the important thing whose rank is rank(x) + r. You can also expect that the sort of node seems in the information structure. Rank seek may be carried out successfully in skip lists, however this requires augmenting the nodes of the skip listing with new information. (b) Define a manner of augmenting pass lists to be able to aid green rank search, and show that your augmentation does not increase the same old excessive-probability order- of-significance time bounds for the SEARCH, INSERT, and DELETE operations.

(c) Now write pseudocode for RANK-SEARCH(x, r) for skip lists. Again expect that each one keys within the skip list are distinct. Assume that the given node x is inside the degree-zero list, and the operation should return a node y in the stage-zero listing. Your set of rules have to run in O(lg m) steps with high opportunity with respect to m = r+1. More precisely, for any high-quality integer ?, your set of rules need to run in O(lg m) time with chance at the least 1 ?1/ ma. Analyze your algorithm carefully.

You are offered with a group of n prizes from that you are allowed to pick at maximum m prizes, where m

(c) As in part (a), there's simplest one form of prize. Give an algorithm that returns a subsequence S = (s1, s2, . . .) of P of length at maximum m, for which j sj .Cost is maximum, difficulty to the brand new constraint that, in S, the values of the prizes ought to shape a non-reducing sequence. Analyze your set of rules in phrases of n and m.

In component (d), the prizes are represented via a rooted binary tree T, with root vertex r, where each vertex u has an related prize, u.Prize. Let P be the set of prizes in the tree. As before, each prize p has a nonnegative integer attribute p.Value. (d) Give an set of rules that returns a fixed S of at maximum m prizes for which s?S s.Value is most, situation to the new constraint that, for any s ? S that is associated with a non-root node u of T, the prize at node u.Determine is also in S. (This means that the selected prizes should be associated with nodes that shape a connected subtree of T rooted at r.)

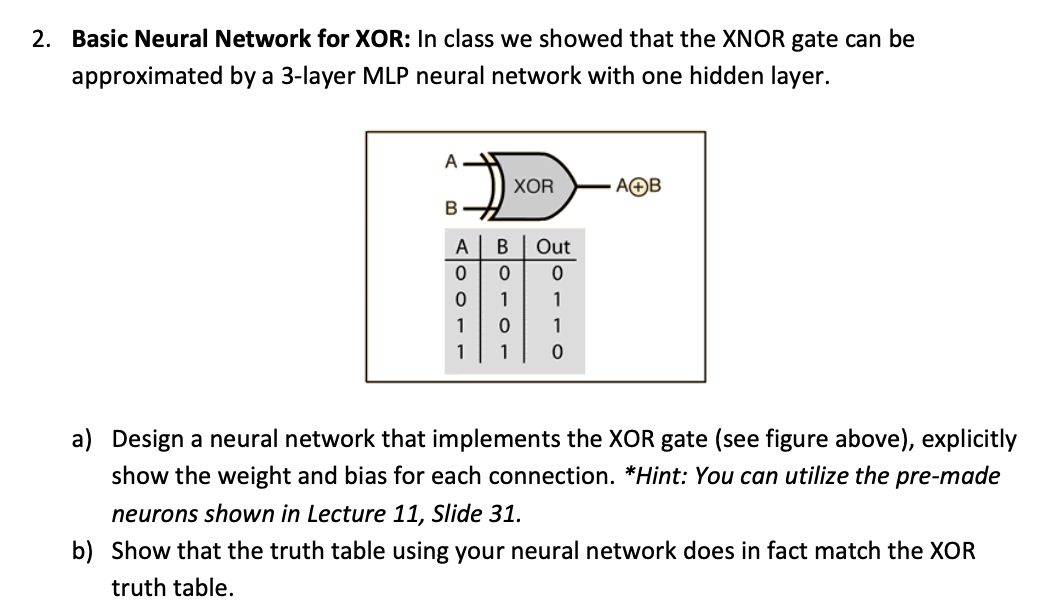
2. Basic Neural Network for XOR: In class we showed that the XNOR gate can be approximated by a 3-layer MLP neural network with one hidden layer. A XOR A+B B A B Out 0 0 0 0 1 1 1 0 1 0 a) Design a neural network that implements the XOR gate (see figure above), explicitly show the weight and bias for each connection. *Hint: You can utilize the pre-made neurons shown in Lecture 11, Slide 31. b) Show that the truth table using your neural network does in fact match the XOR truth table.