Design and implement Floyds algorithm to compute all-pair shortest paths in any given graph using

An adjacency matrix using a one-dimensional array for storing only the elements of the lower triangle in the adjacency matrix.[Using C programming]

The input to program must be connected, undirected, and weighted graphs. The programs must be able to find shortest paths on two types of connected, undirected, and weighted graphs: complete graph (a graph with a link between every pair of nodes) and sparse graph (a graph with exactly n-1 links). To prepare graphs as inputs must include these additional programs (functions) as follows:

1. Random. A program to randomly generate a number between 1 and n. You can use a random number generator function in the libraries of your programming language or write your own function.

2. Complete. A program that can create an adjacency matrix for an undirected complete graph with any given size n.

3. Sparse. A program that can create an adjacency matrix for an undirected sparse graph with any given size n. The Sparse program must use the Random program (number 1 in this list) to determine all the links (n-1) in the sparse graph.

4. Weight. To include weights on the links of the undirected complete graphs (generated by the Complete program, number 2 in this list) and on the links of the undirected sparse graphs (generated by the Sparse program, number 3 in this list), use the Random program (number 1 in this list) to generate positive numbers as weights

Please provide the output for test cases and also the graphs

TEST CASE:

Test case:

adj-test case-1

. . . 29 . . . .

. . . . . 11 11 .

. . . 12 . 5 5 .

29 . 12 . 5 . 13 .

. . . 5 . . 7 11

. 11 5 . . . . 17

. 11 5 13 7 . . .

. . . . 11 17 . .

adj-test case-2

. . . 29 . . . .

. . . . . 11 11 .

. . . 12 . 5 5 .

29 . 12 . 5 . 13 .

. . . 5 . . 7 11

. 11 5 . . . . 17

. 11 5 13 7 . . .

. . . . 11 17 . .

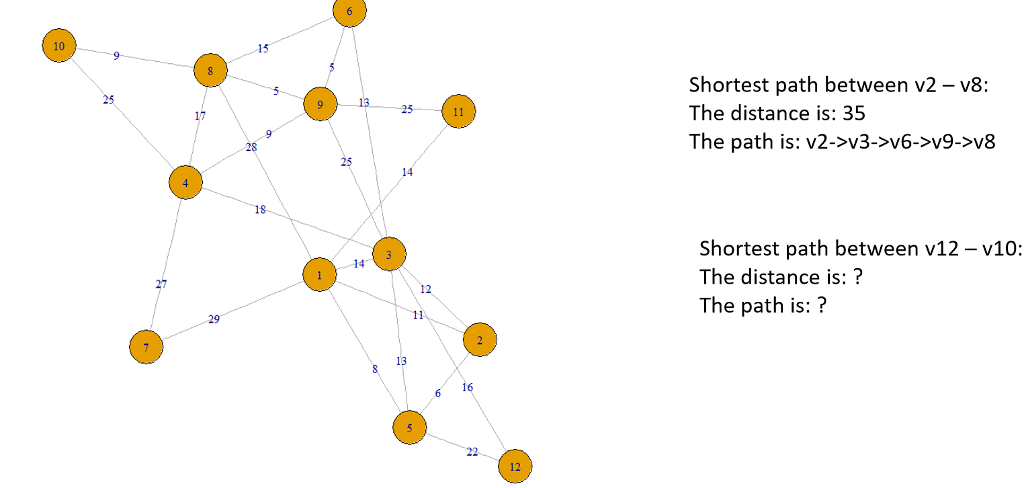
10 15 Shortest path between v2 - v8: The distance is: 35 The path is: v2->v3->v6->v9->v8 13 25 25 17 28 25 14 18 Shortest path between v12-v10: The distance is:? The path is:? 14 12 29 13 16 12