Determine decision strategies based on expected utility for this decision tree. Use the following utility function:

Payoff	Indifference Probability
500	1
350	0.89
300	0.84
180	0.6
100	0.43
40	0.2
20	0.13
0	0

LET U(500)=1 and U(0)=0

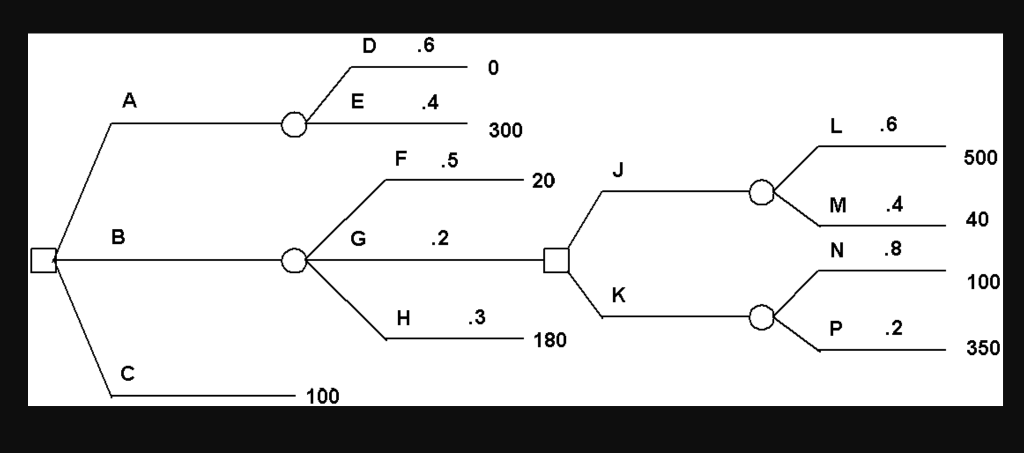
1. What is the expected utility after branch A, i.e., EU( A ) =?

   	A.	0.381
   	B.	0.68
   	C.	0.43
   	D.	0.522
   	E.	0.336

QUESTION 2

1. What is the expected utility after branch J, i.e., EU( J ) =?

   	A.	0.43
   	B.	0.68
   	C.	0.522
   	D.	0.336
   	E.	0.381

QUESTION 3

1. What is the expected utility after branch K, i.e., EU( K ) =?

   	A.	0.336
   	B.	0.522
   	C.	0.43
   	D.	0.381
   	E.	0.68

QUESTION 4

1. What is the expected utility of branch B, i.e., EU( B ) =?

   	A.	0.381
   	B.	0.68
   	C.	0.43
   	D.	0.522
   	E.	0.336

QUESTION 5

1. What is the expected utility after branch C, i.e., EU( C ) =?

   	A.	0.43
   	B.	0.68
   	C.	0.522
   	D.	0.336
   	E.	0.381

QUESTION 6

1. Based on the maximum expected utility approach, what should be the initial decision strategy?

   	A.	Select decision alternative A
   	B.	Select decision alternative B
   	C.	Select decision alternative C

D .6 0 E .4 300 L .6 F .5 500 20 M .4 40 B G .2 N .8 100 K H .3 o .2 180 350 C 100