Question: Determine whether the mapping T is a linear transformation and if so find its kernel. T:P2->P2, where a) T(a0+a1x+a2x^2)=a0+a1(x+1)+a2(x+1)^2 b)T(a0+a1x+a2x^2)=(a0+1)+(a1+1)x+(a2+1)x^2. show T(ku)=kT(u) and T(u+v)-T(u)+T(v)

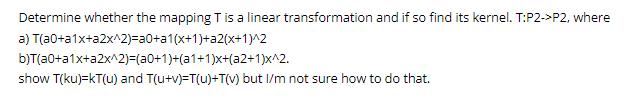
Determine whether the mapping T is a linear transformation and if so

Determine whether the mapping T is a linear transformation and if so find its kernel. T:P2->P2, where a) T(a0+a1x+a2x^2)=a0+a1(x+1)+a2(x+1)^2 b)T(a0+a1x+a2x^2)=(a0+1)+(a1+1)x+(a2+1)x^2. show T(ku)=kT(u) and T(u+v)-T(u)+T(v) but I/m not sure how to do that.

Step by Step Solution

★★★★★

3.48 Rating (148 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

If T: P2 M22 is a linear transformation such that And Find T(5 - 3x + 2x2). . 1 1 1 , T(1 + x) T(1) 1 0.

If L is a linear transformation from V to IV, use mathematical induction to prove that L(a1v1 + a2v2 +...... + anvn) = a1L(V2) + a2L(v2) +.......+ anL(vn)

If T: R R is a linear transformation for which T then: 0-A-0-A 5 and T 5 T([7]) = -5

Determine whether the series is convergent or divergent. If it is convergent, find its sum. 1 3 9. 27 729 81 243

Determine whether the series is convergent or divergent. If it is convergent, find its sum. 1 n-1 4 + e-n

Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. an n sin n n + 1

Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. an 90+1 10"

The system T in Figure is known to be time invariant, when the inputs to the system are x 1 [n], x 2 [n], and x 3 [n], the responses of the system are y 1 [n], y 2 [n], and y 3 [n], as shown. (a)...

The adjusted trial balance of L. Farrish Corporation at May 31, 2014, follows: Requirements 1. Prepare L. Farrish Corporations 2014 single step income statement, statement of retained earnings, and...

Top Notch Frames has asked you to determine whether the companys ability to pay current liabilities and total liabilities improved or deteriorated during 2014. To answer this question, compute these...

Identify each of the following as they pertain to the SEC. a. Blue sky laws. b. S8 Statement. c. Letter of comments. d. Public Company Accounting Oversight Board. e. Prospectus.

Who is the most important user of an auditors report on a companys financial statements: company management, the companys shareholders, or the companys creditors? Briefly explain your rationale and...

A project has the following time schedule. \ table [ [ Activity , Time ( months ) ] , [ 1 - 2 , 2 ] , [ 1 - 3 , 2 ] , [ 1 - 4 , 1 ] , [ 2 - 5 , 4 ] , [ 3 - 6 , 8 ] , [ 3 - 7 , 5 ] , [ 4 - 6 , 3 ] , [...

a) Draw the structure of an Omega-5 fatty acid with an 14:2 designation. b) Provide a reaction for the partial hydrogenation of the fatty acid in Question 1(a). Is the product that forms still an...

E (V/m) 0 2.5 cm B. Cylindrical capacitor: A 1 m long, cylindrical capacitor is made of a metal rod inside of a metal tube as shown in cross section above. The rod has a diameter of 2 cm and the tube...

content area top Part 1 Find the indicated probabilities using the geometric distribution, the Poisson distribution, or the binomial distribution. Then determine if the events are unusual. If...

I. Consider the following mapping diagrams. (a) For each mapping diagram {diagram with dots and arrows) in Figure 1.3, determine whether the diagram gives a function from A to B. (b) What easytospot...

( a ) Determine whether the mapping f : Q Q defined by f ( m n ) = m 2 n , AAm,ninZ, n 0 is well defined function. Justify your answer. ( b ) Let f : ( R ? ? { 1 } ) ( R ? ? { 1 } ) be a function...

Determine whether the mapping represented a function. Name Birthday Rebecca Jennifer January 18 John February 15 Hector April 1 Luis April 7 Ebony June 23 Raphael July 30 Meredith Karen Joseph August...

Determine whether the mapping represented a function. Name Birthday Amy January 5 Carol Devon January 7 February 24 Harrison March 1 Jackson April 7 Labron May 30 Mason July 20 Natalie - August 1...