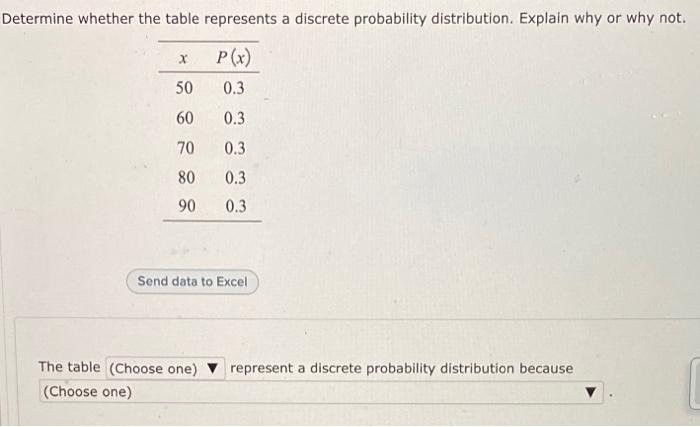
Determine whether the table represents a discrete probability distribution. Explain why or why not. P(x) 0.3 0.3 0.3 0.3 0.3 x 50 60 70 80 90 Send data to Excel The table (Choose one) (Choose one) represent a discrete probability distribution because Develop a simplified model based on a fixed mass reactor for the analysis of combustion in an internal combustion engine. Assume that the reaction of the fuel with the oxidant takes place in a single step with the following stoichiometric mass coefficients: 1 kgF + u kgOx (1+U) kg Pr and with the following reaction rate: wF = -A exp(-Ea / Ru-T) [F]m [Ox]n, whose constants are given by Table 5.1 (Turns, 2013). Also assume the simplified thermodynamic properties: MF = MOx = Mpr. Cp,F = Cp, Ox = Cp,Pr, hf, Pr = hf,0x = 0 and hff = Ah. Specific heats do not vary with temperature. Your model must be able to evaluate transient temperature, concentrations and pressure or volume, depending on the type of reactor chosen. Assume the engineering assumptions necessary for the solution. It is not necessary to solve your model computationally, just explain your equations in terms of the unknowns T, YF, YOX and YPr only. Attention, these should be the only unknowns that should appear in your solution. Create a table to enter the values of the constants needed for the calculation. Identify the conditions for which your model must be developed in the table below. Engine cycle --> Diesel Fuel --> C10H22