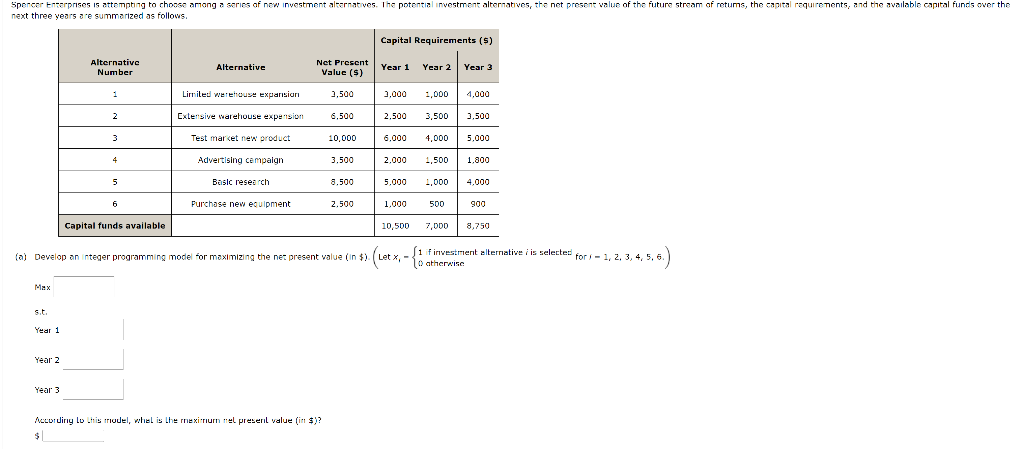
) Develop an integer programming model for maximizing the nez present value (in $) ( Let x1{1firivestmentalterrativeiisselected0atheraise P-lax s.t. Year 1 Year 2 Year 3 Actoidirig to .this rrodel, whel is the roexi-rium "nl preseril value (iin $ ?? $ (b) Assume that only one of the warehouse expansion projects can be Implemented. Modify your model from part (a). In addition to the constraints from part (a), what additional constraint should be added to the integer programming model? According to this model, what is the maximum net present value (in $ )? $ (c) Suppose that if test marketing of the new product is carried out, the advertising campaign also must be conducted. Modify your formulation from part (b) to reflect this new situation. In addition to the constraints from part (a) and part (b), what additional constraint should be added to the integer programming model? According to this model, what is the maximum net present value (in \$)? $ ) Develop an integer programming model for maximizing the nez present value (in $) ( Let x1{1firivestmentalterrativeiisselected0atheraise P-lax s.t. Year 1 Year 2 Year 3 Actoidirig to .this rrodel, whel is the roexi-rium "nl preseril value (iin $ ?? $ (b) Assume that only one of the warehouse expansion projects can be Implemented. Modify your model from part (a). In addition to the constraints from part (a), what additional constraint should be added to the integer programming model? According to this model, what is the maximum net present value (in $ )? $ (c) Suppose that if test marketing of the new product is carried out, the advertising campaign also must be conducted. Modify your formulation from part (b) to reflect this new situation. In addition to the constraints from part (a) and part (b), what additional constraint should be added to the integer programming model? According to this model, what is the maximum net present value (in \$)? $