Differentiation: Composite, Implicit, and Inverse Functions

References by topic below:

27	0(3.01) The Chain Rule Segment: 1
28	0(3.02) Implicit Differentiation Segment: 1
29	0(3.03) Differentiating Inverse Functions Segment: 1

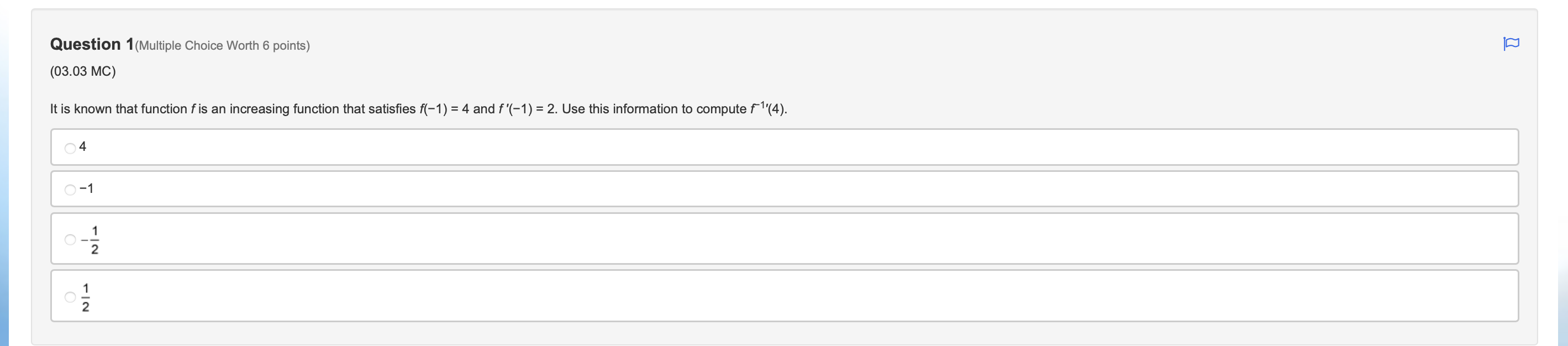
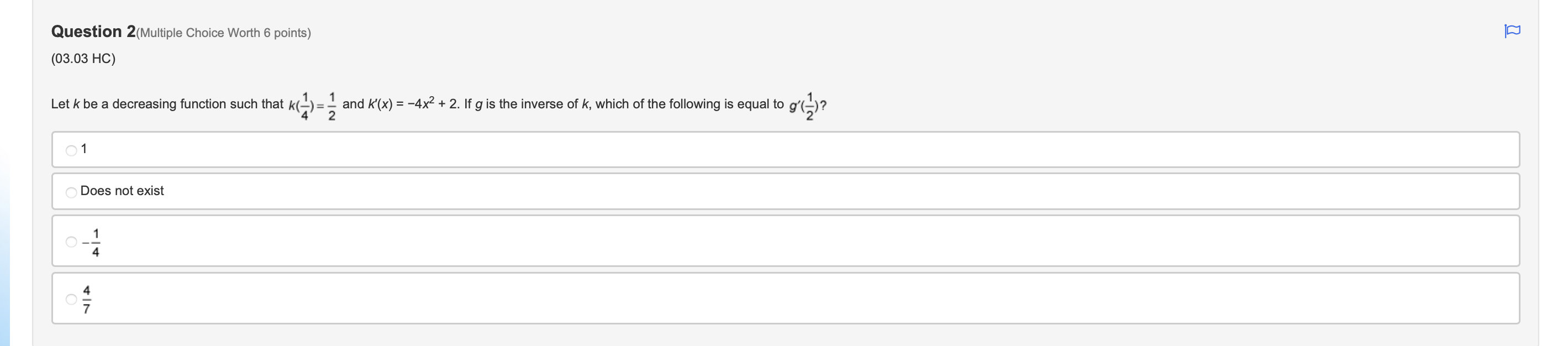
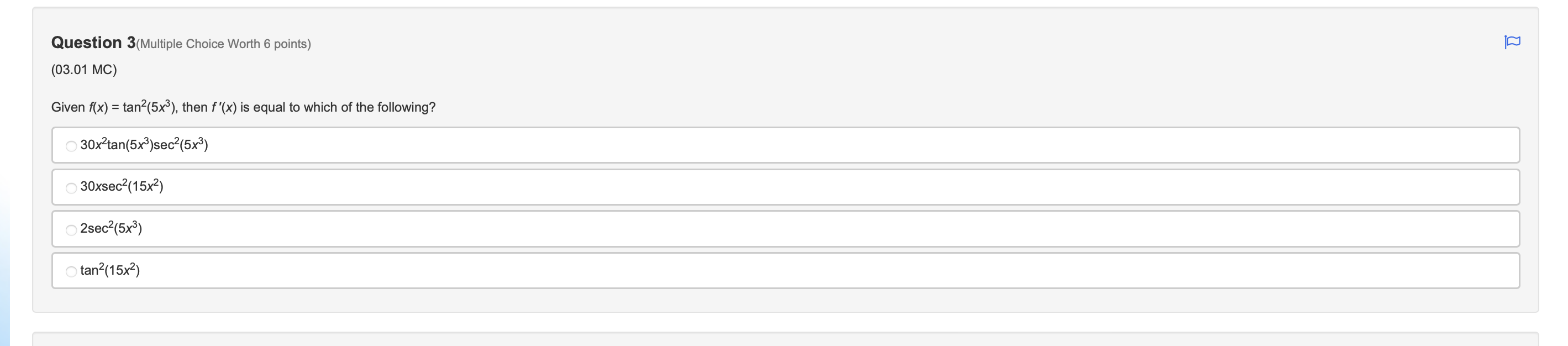
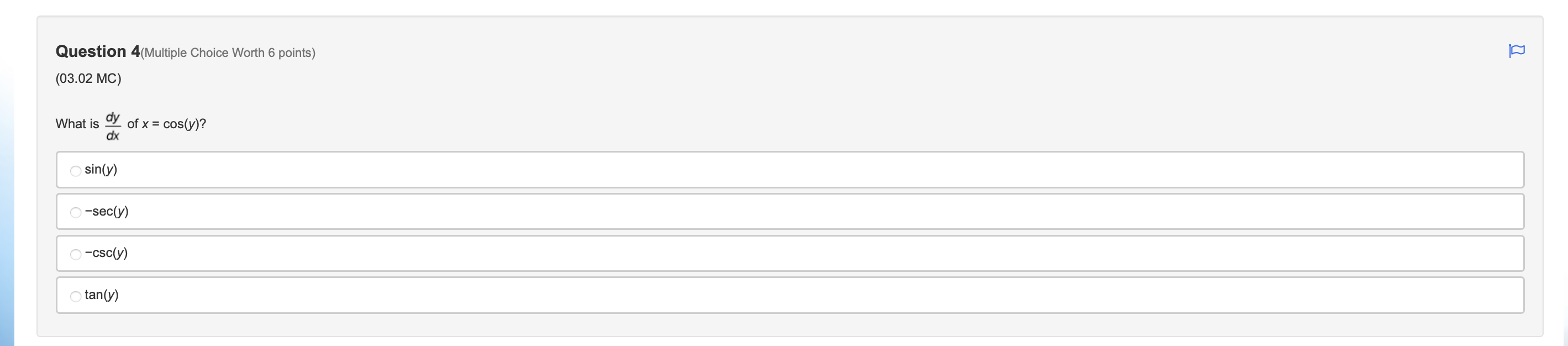
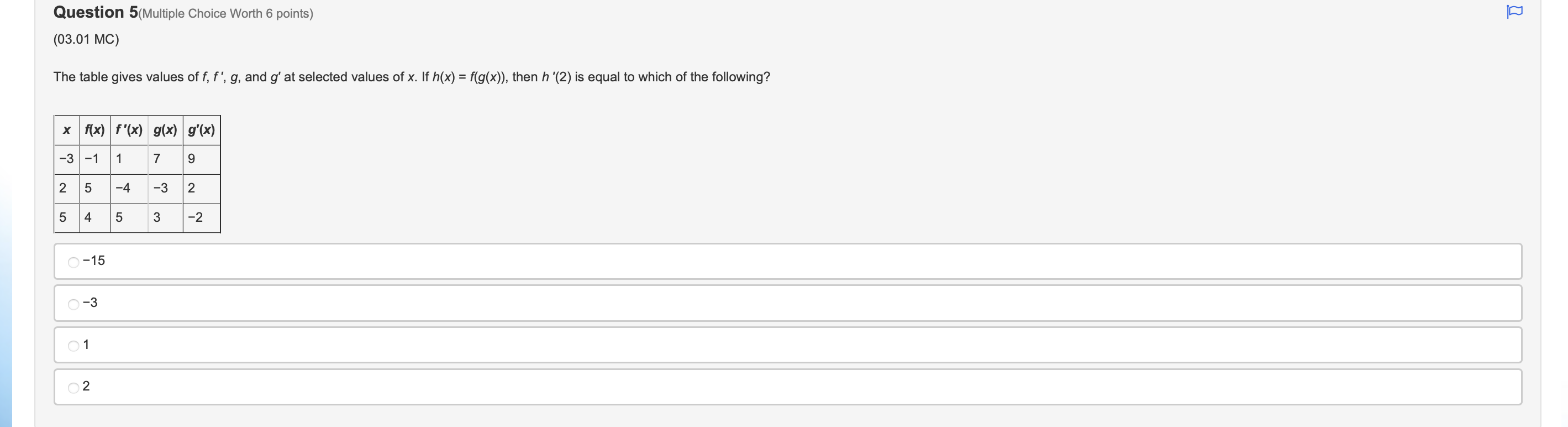
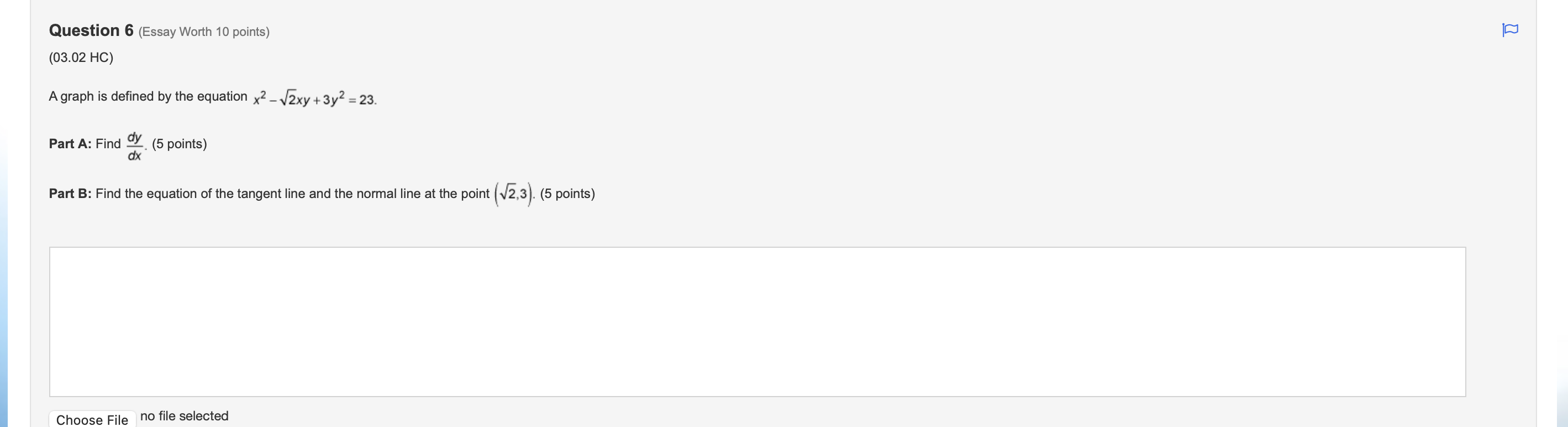
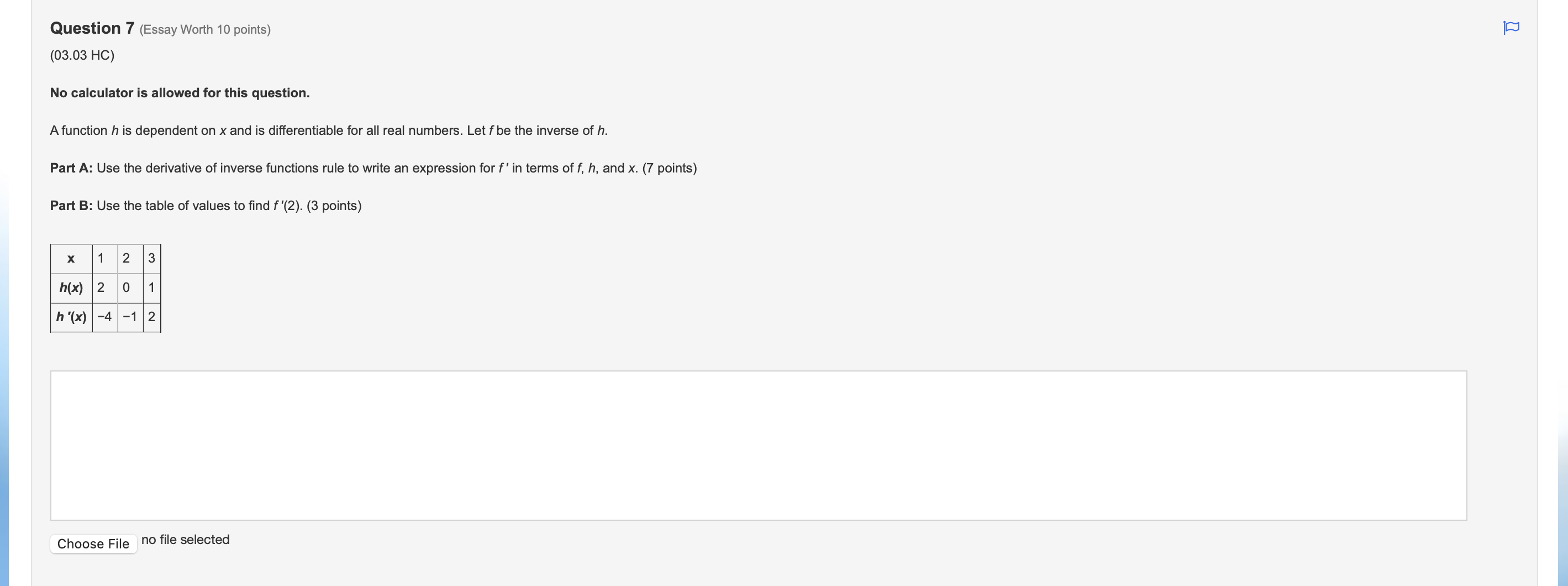
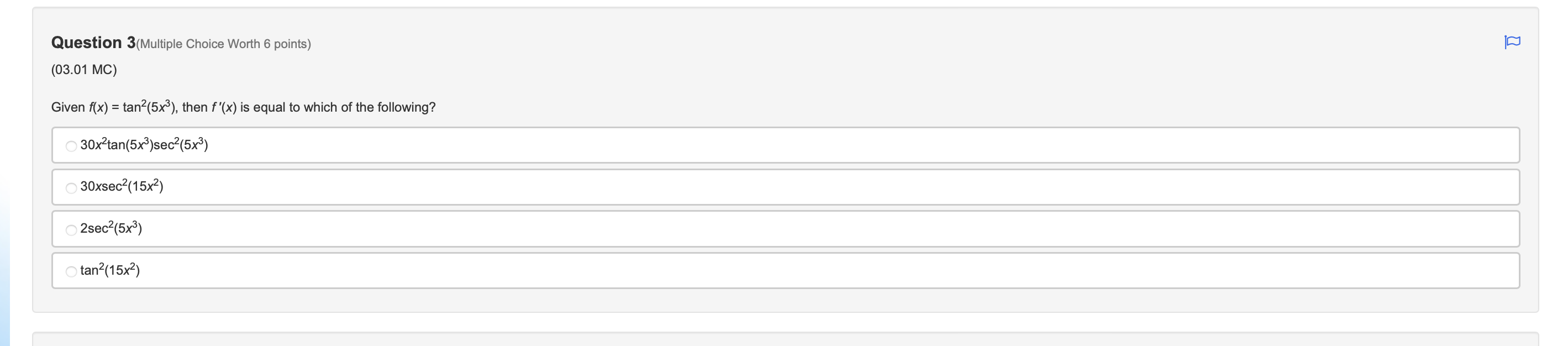
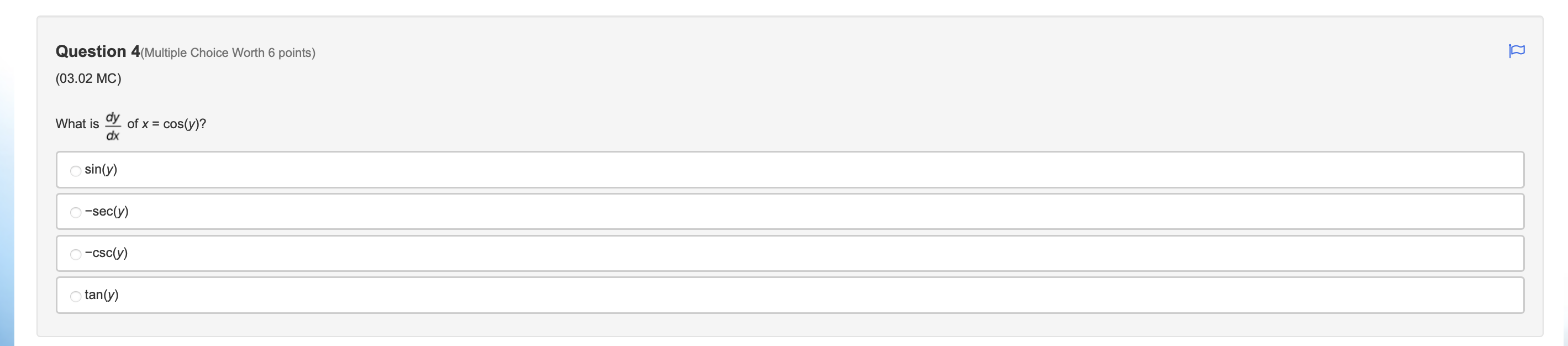
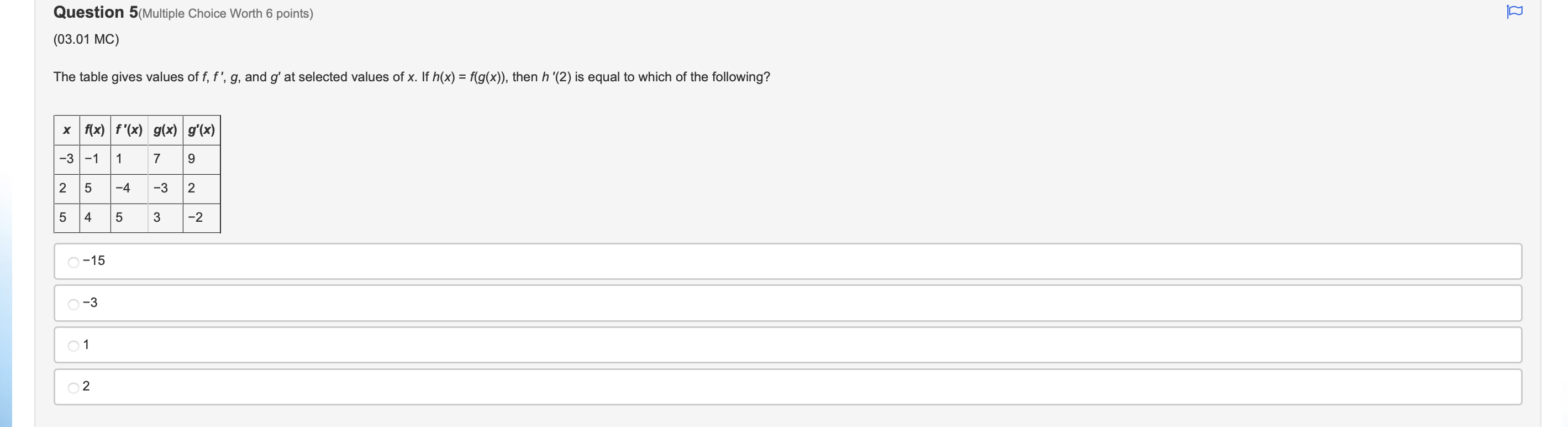
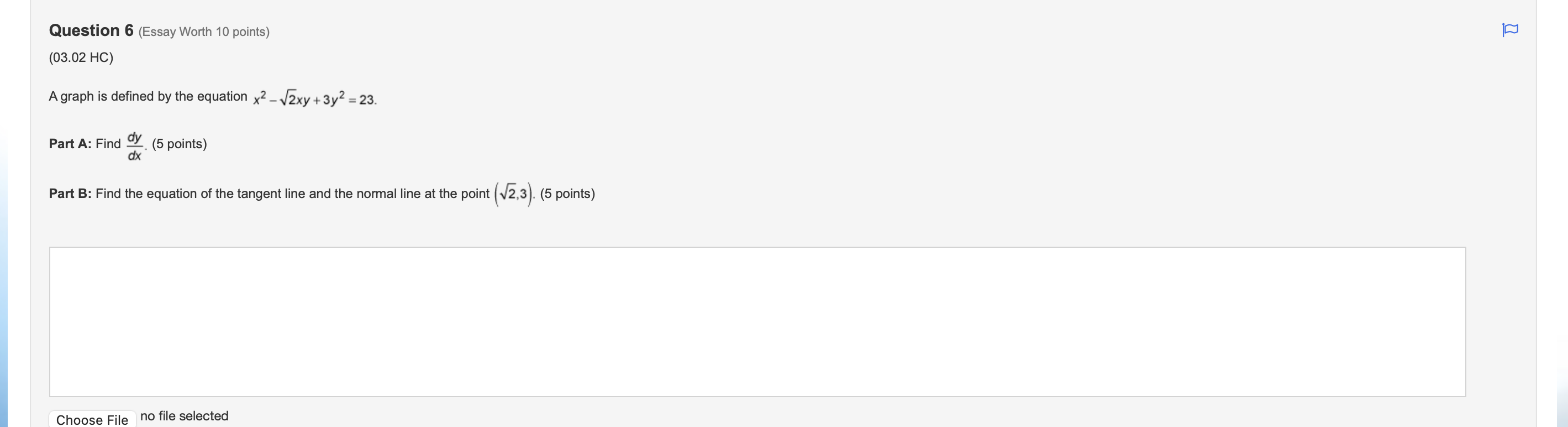
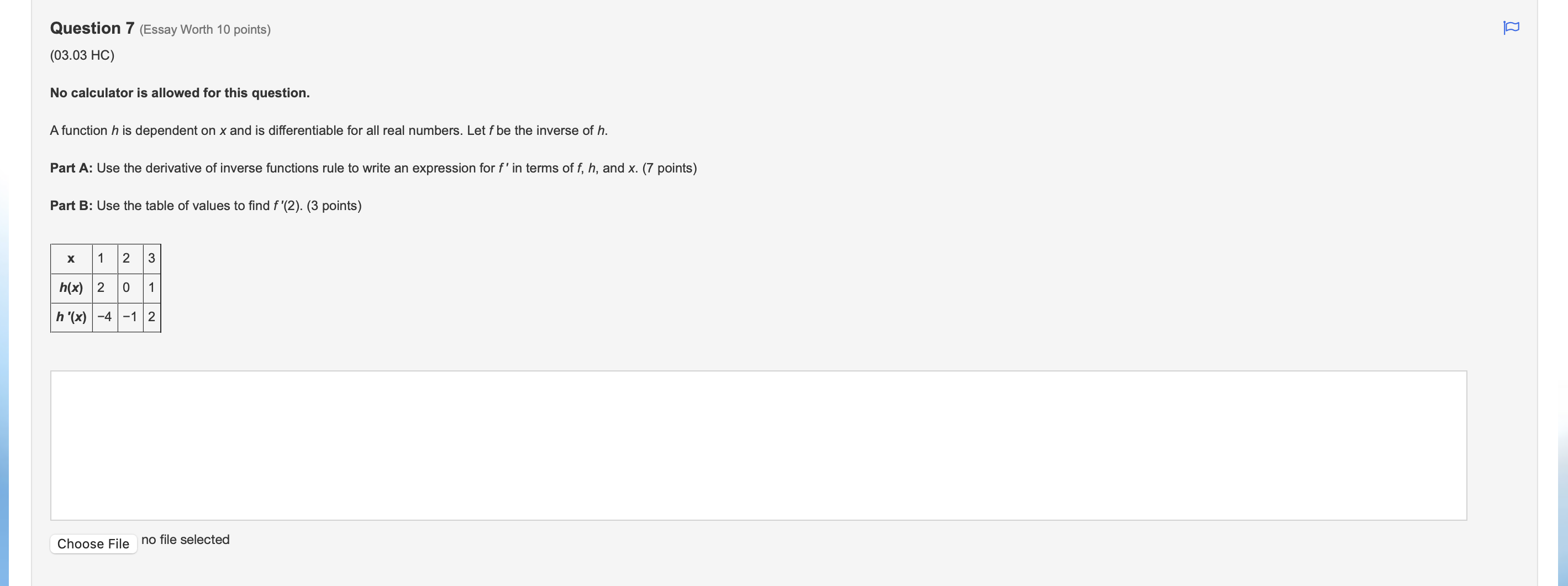
Question 1(Multiple Choice Worth 6 points) (03.03 MC) It is known that function f is an increasing function that satisfies f(-1) = 4 and f'(-1) = 2. Use this information to compute f1'(4). )4 O-1 O N/ - N/-Question 2(Multiple Choice Worth 6 points) (03.03 HC) Let k be a decreasing function such that k(-) = - and k'(x) = -4x2 + 2. If g is the inverse of k, which of the following is equal to g'(-)? Does not exist O Al O VIAQuestion 3(Multiple Choice Worth 6 points) (03.01 MC) Given f(x) = tan2(5x3), then f'(x) is equal to which of the following? 30x2tan(5x3)sec2(5x3) 30xsec2(15x2) 2sec2(5x3) O tan2(15x2)\fQuestion 5(Multiple Choice Worth 6 points) (03.01 MC) The table gives values of f, f', g, and g' at selected values of x. If h(x) = f(g(x)), then h '(2) is equal to which of the following? x f ( x) f' ( x) g(x) g' (x ) -3 -1 1 7 S 2 -4 2 5 4 5 3 -2 O-15 O -3 O1 O2Question 6 (Essay Worth 10 points) (03.02 HC) A graph is dened by the equation X2 , ny + 33/ = 23 Part A: Find %. (5 points) Part B: Find the equation of the tangent line and the normal line at the point (J53) (5 points) Choose File no file selected [D Question 7 (Essay Worth 10 points) (03.03 HC) No calculator is allowed for this question. A function h is dependent on x and is differentiable for all real numbers. Let f be the inverse of h. Part A: Use the derivative of inverse functions rule to write an expression for f' in terms of f, h, and x. (7 points) Part B: Use the table of values to find f'(2). (3 points) X 2 3 h(x) 2 0 1 h'(x) -4 2 Choose File no file selected