Question: Directions: Consider the following function f(x) at a=2 f(x)=4x24 Part 1 - Difference Quotient If h=0, then the difference quotient can be simplifed into the

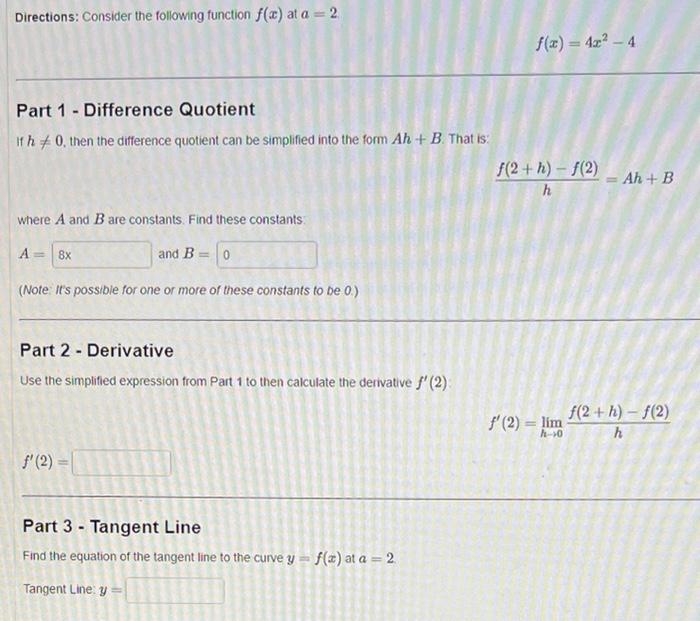
Directions: Consider the following function f(x) at a=2 f(x)=4x24 Part 1 - Difference Quotient If h=0, then the difference quotient can be simplifed into the form Ah+B. That is: hf(2+h)f(2)=Ah+B where A and B are constants. Find these constants: A=andB= (Note: its possible for one or more of these constants to be 0 .) Part 2 - Derivative Use the simplified expression from Part 1 to then calculate the derivative f(2). f(2)=limh0hf(2+h)f(2) f(2)= Part 3 - Tangent Line Find the equation of the tangent line to the curve y=f(x) at a=2. Tangent Line: y=

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

Directions Consider the following function f x at a 3 Part 1 Difference Quotient A If h0 then the difference quotient can be simplified into the form f 3 h f 3 h where A B C D and E are all non...

Directions Consider the following function f x at a 8 Part 1 Difference Quotient If h 0 then the difference quotient can be simplified into the form f 8 h f 8 8 h where A and B are constants Find...

Directions Consider the following function f a at a 2 Part 1 Difference Quotient If h0 then the difference quotient can be simplified into the form 2 A f 2 h where A B and C are all non negative...

Directions Consider the following function f z at a 2 Part 1 Difference Quotient It h 0 then the difference quotient can be simplified into the form Ah B That is 2 h f 2 Ah B h where A and B are...

Directions: Consider the following function f(x) at a=1 .\ f(x)=x-5 \ Part 1 - Difference Quotient\ If h!=0 , then the difference quotient can be simplified into the form Ah+B . That is:\...

Directions Consider the following function where A and B are constants Find these constants A and Part 1 Difference Quotient If x 1 then the difference quotient can be simplified into the form Ax B...

%% Lab 2 - Your Name - MAT 275 Lab %% Example code % Example 1 % NOTE: Delete examples before submission. A = [1 0; 0 -1] A = [1, 0; 0, -1] % NOTE: The two matrices above are the same. We can...

Image transcription text Module 5 Discussion A' Instructions: This discussion will be completed in two parts, and will give you an opportunity to reect upon this week's content and to interact with...

Score on last try: 0 of 1 pts. See Details for more. Get a similar question You can retry this question below Use the limit definition of the derivative to find the slope of the tangent line to the...

Using Python, In this assignment, we will analyze the HURDAT2 dataset for Atlantic hurricane data from 1851 through 2017. This dataset is provided by the National Hurricane Center and is documented...

Ropes AB and AC are thrown to a boater whose canoe had capsized. Knowing that α =25° and that the magnitude of the force FR exerted by the river on the boater is 70 lb, determine the...

The chief audit executive (CAE) establishes ______ to guide the internal audit function in a systematic manner

udio Escape Inc. manufactures audio speakers. Each speaker requires $125 per unit of direct materials. The speaker manufacturing assembly cell includes the following estimated costs for December: 1...