Discrete mathematics for computing

Q.

Modify the ALGORITHM in example 1.3.1 so that it gives the correct output when n=0 is input. Please show clear work.

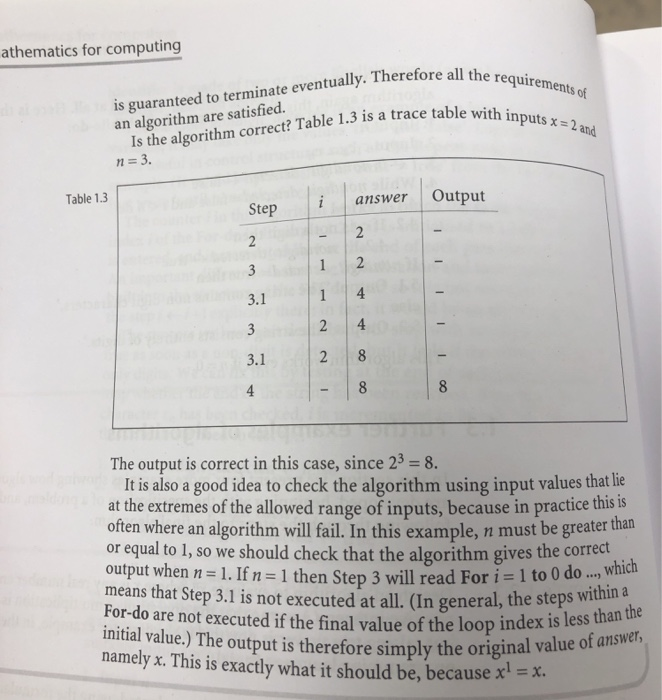
1.3 Further examples of algorithms In this section, we present four more examples showing how algorithms are developed, beginning with the specification of a problem, and following through the steps to the final algorithm. Example 1.3.1 Design an algorithm to evaluate x", where x is any real number and n is a positive integer. (Assume that the operation of multiplication is available, but raising to a power is not; this is the case, for example, in the programming language Pascal.) Solution If n is a positive integer,x" can be evaluated using the formula: x = xxxx...XX n times In order to carry out this process, we will need a variable answer, which is initially assigned the value of x, and which is then multiplied by x the required number of times. The number of multiplications is fixed at n - 1, so a For-do loop is the most appropriate control structure to use here. 1. Input x, n 2. answer X 3. For i = 1 to n - 1 do 3.1. answer answer x x 4. Output answer Is this sequence of steps an algorithm? The steps are clear and unambiguous, they are executed in a clearly defined sequence, and Step 3.1 in the For-do loop is executed a finite number of times, so the process athematics for computing ore all the requirements of ce table with inputs x = 2 and is guaranteed to terminate eventually. Therefore all th an algorithm are satisfied. Is the algorithm correct? Table 1.3 is a trace table n=3. Table 13 answer Output Step oo oo * ANN 4 The output is correct in this case, since 23 = 8. It is also a good idea to check the algorithm using input values that lie at the extremes of the allowed range of inputs, because in practice this is often where an algorithm will fail. In this example, n must be greater than or equal to 1, so we should check that the algorithm gives the correct output when n= 1. If n= 1 then Step 3 will read For i = 1 to 0 0 means that Step 3.1 is not executed at all. (In general, the step is less than the secuted if the final value of the loop index is less than the d For i = 1 to 0 do ..., which all. (In general, the steps within a For-do are not executed if the final value of u namely x. This is exactly what it should be, because x e simply the original value of