divide and conquer. promot is below and i keep getting the wrong output. i have attached the prompt, my code, and the test cases(input and output files). please actually help acheive correct results and not just copy off chatgpt. will give thumbs up!!!!

prompt

code so far

test cases i have to get correct

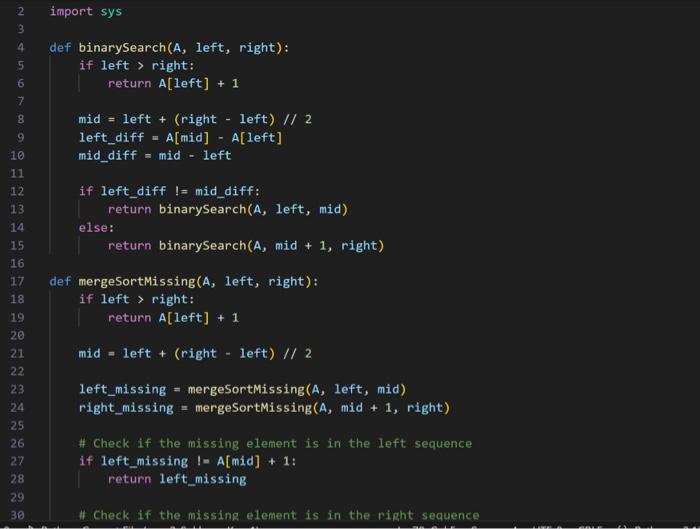
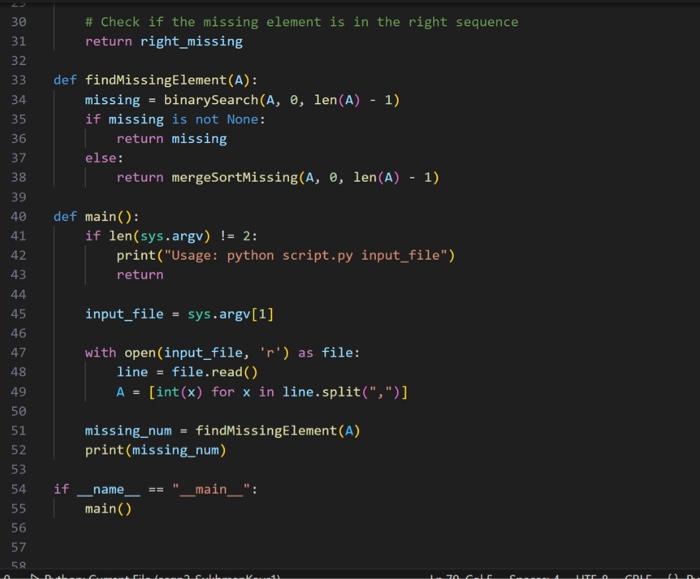
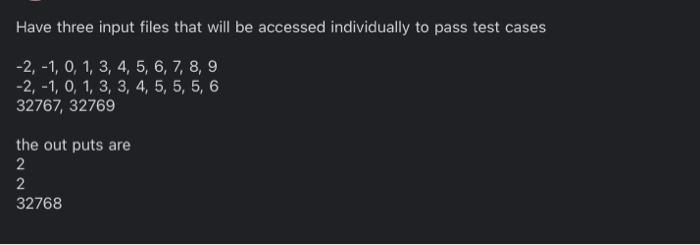
Part 1: Finding Missing Elements Suppose that you are given a sorted sequence of multiple integers, within which exactly one of the possible integers (that is, the integers between the first and last elements) is missing. For example: (1,:2,4;,5,6,7,8) Note that, because the sequence is sorted, any succesive elements must appear consecutively. As a result, the missing element could be found naively in linear time simply by iterating over the elements of the sequence, checking each clement to see if it differs by 1 from those immediately before and after. Part 2: A Binary-Search-Based Approach Further suppose you know that, within the given sequence, all elements are distinct. Exactly one element within the possible range does not appear; no element appears two or more times. For example: (2,1,0,1,3,4,5,6,7,8,9) In the above sequence, the missing element is 2 . In this situation, it should be possible to discard subproblems which cannot possibly be missing an element, in a manner similar to that of binary search. Design and analyze (but do not yet implement) a divide and conquer algorithm to find the missing element within a sorted sequence of multiple integers, where elements must be distinct. Your algorithm should have complexity O(logn), having avoided a substantial amount of potential work. Part 3: A Merge-Sort-Based Approach Now suppose, as a generalization of the above examples, that elements nexd not be distinct, and could potentially appear two or more times. For example: (2,1,0,1,3,3,4,5,5,5,6) In the above sequence, the missing dement remains 2. However, in order to find it, it is no longer possible to determine (at least not generally and in constant time) which subproblems must necessarily contain all possible elements. As a result, all subproblems must be solved, in a manner similar to that of merge sort. Such an algorithm would have complexity O(n), having achieved no improvement over a naive algorithm. You now have two approaches for solving this problem: one that sometines works in logarithmic time, and one that aluays works in linear time. Recall that when two functions are added together, the larger eventually dominates the sum: O(logn)+O(n)=O(n). That is to say, there is no asymptotic petialty to simply trying, the logarithmic algorithm first 1. Put another way, the linear algorithm was going to recurse on all subproblems regardless, so there is no penalty to using the logarithmie algorithm's approach in deciding which subproblem to recurse on first. If the logarithmic algorithm can find the missing element, you have solved the problem in O(logn) time. If it cannot, you can fall buck on the linear algorithm, thereby solving the problem in a combined O(n) time. In your programming language of choice (see Assignment 1), implement a divide and conquer algorithm to find the missing element of a given sequence: - Your implementation must first attempt to solve the problem in binary-search-based logarithmic time. - Your implementation must resort to merge-sort-based linear time if and only if that first attempt fails. In order to incorporate the linear approach, your implementation will likely deviate from your logarithmic pseudocode designed in Part 2. You may assume that all sequences will contain multiple comma-separated integers, sorted in ascending order, such that exactly one of the possible integers does not exist as an element. For example, the second of the above sequences would be represented as: 2,1,0,1,3,4,5,6,7,8,9 Your program must accept as a command line argument the name of a file containing a sequence as described above, then print to stdout the missing element. For example: >$./compile.sh>$./run.shin1.txt2 Your program will be tested using diff, so its printed output must match cractly. import sys def binarySearch (A, left, right): if left > right: return A[ left ]+1 mid =1 eft +( right 1eft)//2 left_diff =A[ mid ]A[left] mid_diff = mid 1eft if left_diff 1= mid_diff: return binarySearch(A, left, mid) else: return binarySearch (A, mid +1 , right) def mergeSortMissing( A, left, right): if left > right: return A[ left] +1 mid =1eft+(right1eft)//2 left_missing = mergeSortMissing ( A,1eft, mid ) right_missing = mergeSortMissing (A,mid+1, right ) \# Check if the missing element is in the left sequence if left_missing I=A[mid]+1 : return left_missing Al Check if the missing element is in the pight sequence \# Check if the missing element is in the right sequence return right_missing def findMissingElement(A): missing =binarySearch(A,0,len(A)1) if missing is not None: return missing else: return mergeSortMissing(A, 0,len(A)1) def main() : if 1 en(sys.argv) !=2 : print("Usage: python script.py input_file") return input_file = sys.argv[1] with open(input_file, ' r ') as file: line = file read() A=[int(x) for x in line.split (",")] missing_num = findMissingElement (A) print(missing_num) if _ name__ ==" __main__" : main() Have three input files that will be accessed individually to pass test cases 2,1,0,1,3,4,5,6,7,8,92,1,0,1,3,3,4,5,5,5,632767,32769 the out puts are 2232768