Do NOT copy answers from others or else thumb DOWN!

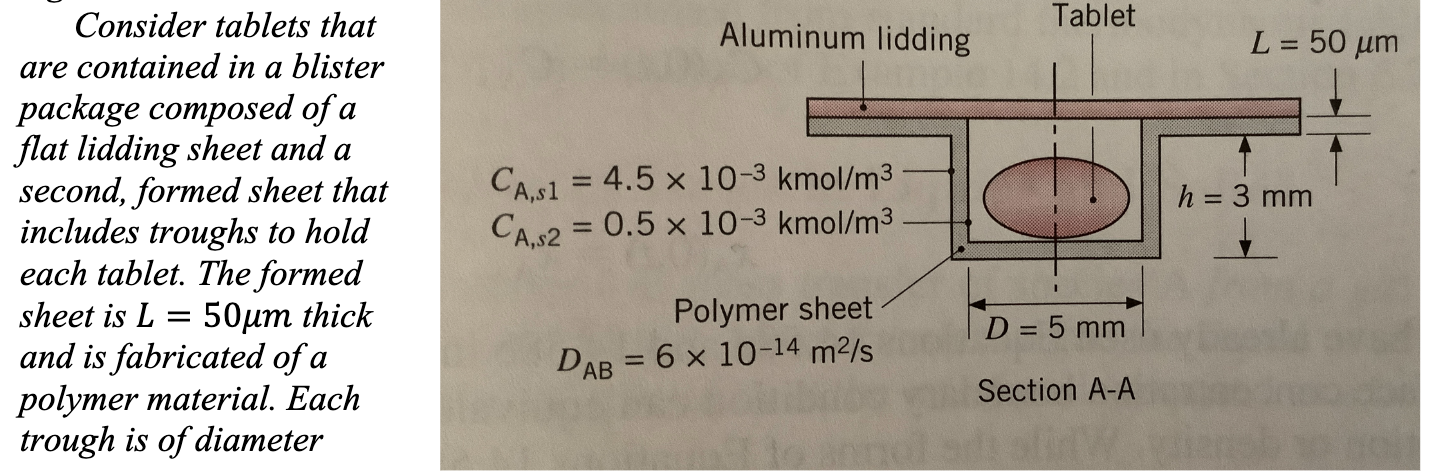
Consider tablets that are contained in a blister package composed of a flat lidding sheet and a second, formed sheet that includes troughs to hold each tablet. The formed sheet is L=50m thick and is fabricated of a polymer material. Each trough is of diameter D=5mm and depth h=3mm. The lidding sheet is fabricated of aluminum foil. The binary diffusion coefficient for water vapor in the polymer is DAB=61014m2/s while the aluminum may be assumed to be impermeable to water vapor. Do not include the presence of the pill in your analysis. (a) What would the boundary condition be at the surface inside the "blister", immediately under the aluminum lidding? (b) In this problem there are three regions: inside the blister, outside the blister, and in the polymeric wall material surrounding the blister. Based on an order of magnitude analysis, which of these regions will transport be slowest? This slowest region will control the rate of transport overall, and it forms the domain in which the governing transport equation should be solved. (c) Assume that the concentration inside the blister is constant, and there is perfect mixing outside the blister wall. This sets the molar concentrations of water vapor in the polymer at the outer and inner surfaces to constant values CA,s1=4.5103kmol/m3 and CA,s2= 0.5103kmol/m3, respectively. Determine the rate at which water vapor is transferred through the trough wall to the tablet. You should recognize that the transport across the vertical walls and horizontal base of the polymeric material can be split into two, independent, 1D transport problems that meet the boundary conditions. The vertical walls may be treated as flat films, since their thickness LD/2