Do the following in MATLAB code by using below format as example. Please show code.

a= 0; % Left endpoint of integral b= pi; % Right endpoint N = 10; % The number of sub-intervals (|N| must be even for h=(b-a)/N; x= a:h:b; % Creates a vector of N+1 evenly spaced points between |a| and |b| f=sin(x); % The function to integrate Iexact = 2; % The exact integral Itrapezoid=0; Isimpson=0; for k=1:N %Note that the vector f has (N+1) elements Itrapezoid=Itrapezoid+h*(f(k)+f(k+1))/2; end; for k=1:(N/2) Isimpson=Isimpson + h/3*(f(2*k-1)+4*f(2*k)+ f(2*k+1)); end fprintf(' Exact integral = %f. ', Iexact) fprintf(' Trapezoidal approximation = %f. ',Itrapezoid); fprintf(' Simpson approximation = %f. ',Isimpson); fprintf(' ') fprintf(' Trapezoidal error = %f. ',abs(Itrapezoid-Iexact)); fprintf(' Simpson error = %f. ',abs(Isimpson-Iexact)); % Output from this program:

Q: Approximate the integral of

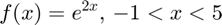
Answer the following questions

• Run the code with N=16, N=32, and N=64.
• For each approximation, when does the result agree with the exact value of the integral to 4 digits?
• How much better is the Simpson's rule than the trapezoidal rule? Explain this result using the theory given in the textbook and in lecture. Be quantitative. Calculate the ratios between the errors each time the number of points is doubled.

f(z) = e2",-1