Double integrals over general regions problems

Exercise 5.2(4,6,7,10)

Calculus 3

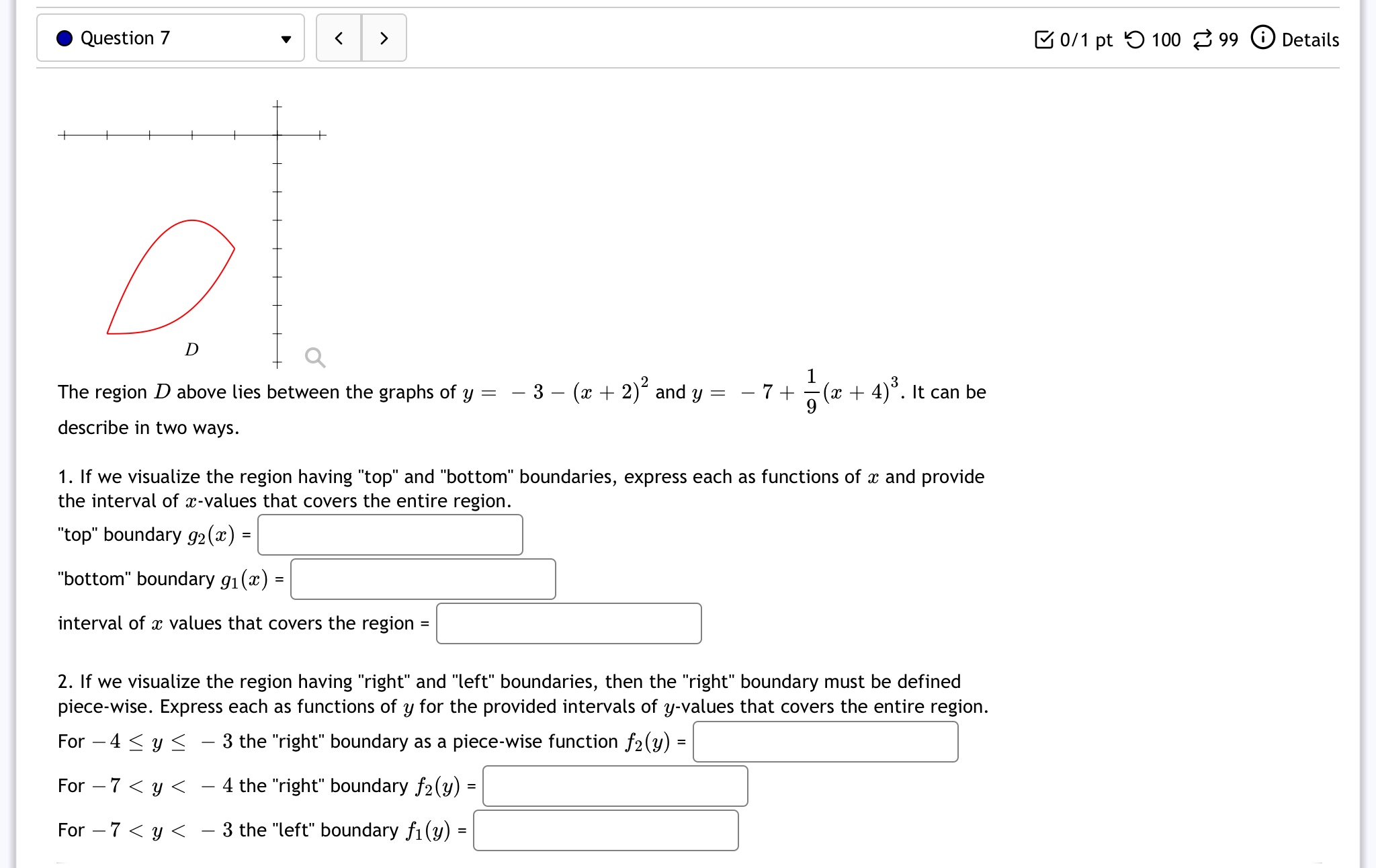
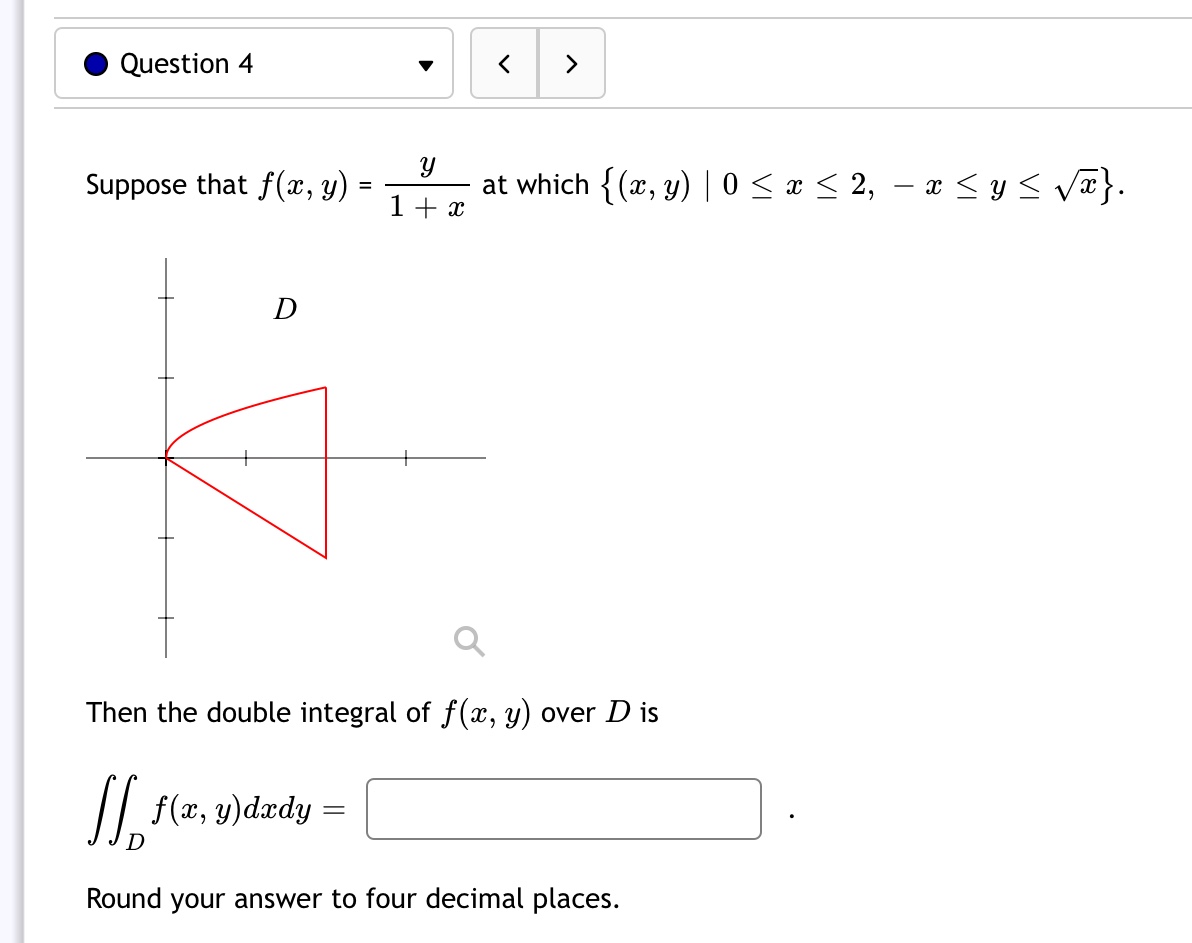
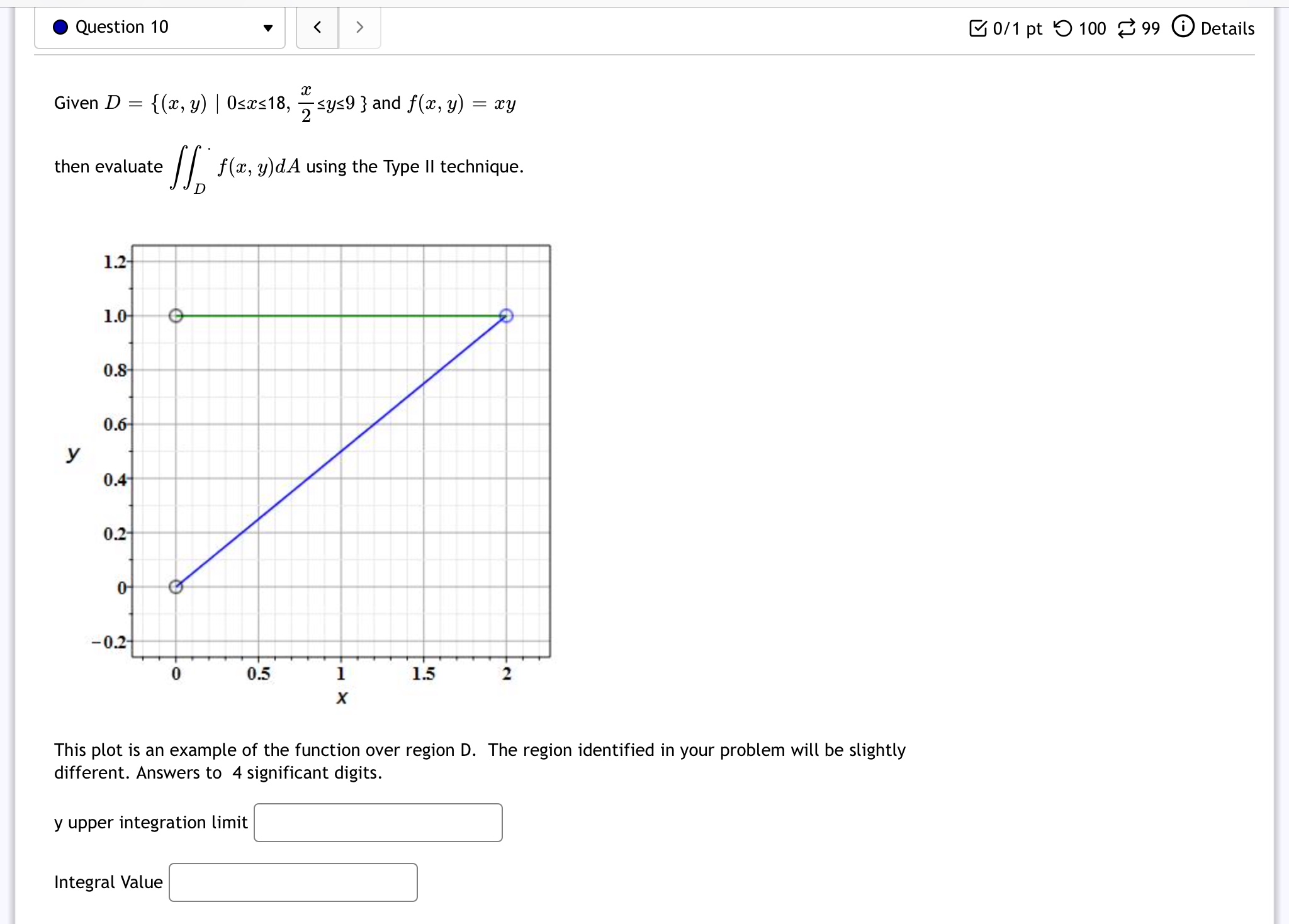
0 Question 7 v D Q 1 The region D above lies between the graphs of y = 3 (z + 2)2 and y = 7 + 5(w + 4)3. It can be describe in two ways. 1. If we visualize the region having "top" and "bottom" boundaries, express each as functions of w and provide the interval of w-values that covers the entire region. interval of a: values that covers the region = :] 2. If we visualize the region having "right" and "left" boundaries, then the "right" boundary must be defined piece-wise. Express each as functions of y for the provided intervals of y-values that covers the entire region. For 4 S y S 3 the "right" boundary as a piece-wise function f2(y) = :] For 7 Suppose that one variable, 2:, is chosen randomly and uniformly from [0, 1], and another variable, y, is also chosen randomly and uniformly from [0, 3]. What is the probability that :1: S y S 33: + 1? The probability for a: g y S 323 + 1 is Round your answer to four decimal places. 0 Question 4 v Suppose that f(:c,y) = at which {(3), y) l 0 S a: g 2, a: S y 3 }. 1+3: q Then the double integral of f(a:, y) over D is [@wa Round your answer to four decimal places. I Question 10 v ' 30/1 pt 0100 399 Ooetails Given D = {(93, y) I 0595518, g5y59}and f(w,y) = my then evaluate ff f (w, y)dA using the Type II technique. D This plot is an example of the function over region D. The region identified in your problem will be slightly different. Answers to 4 significant digits