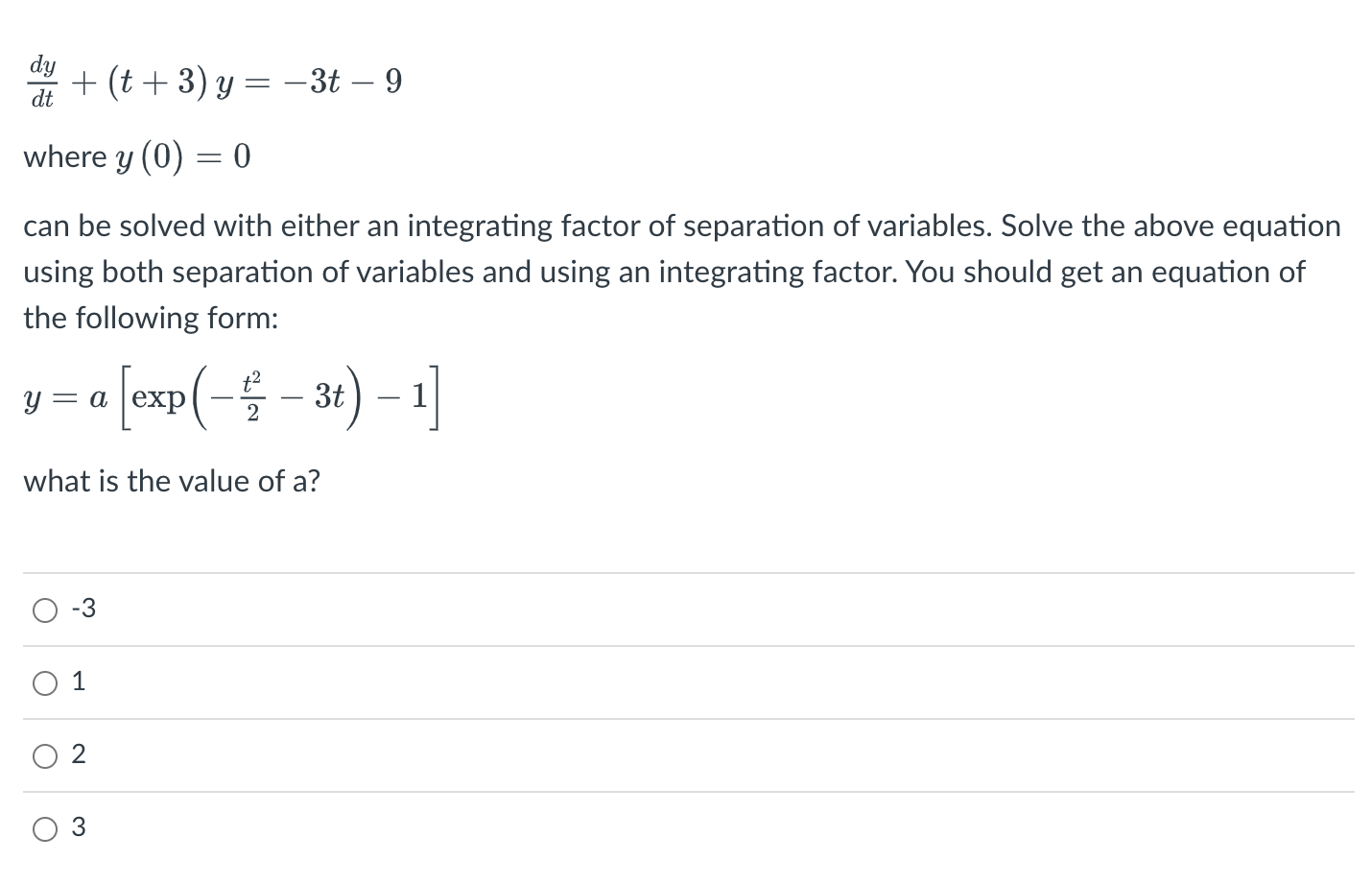
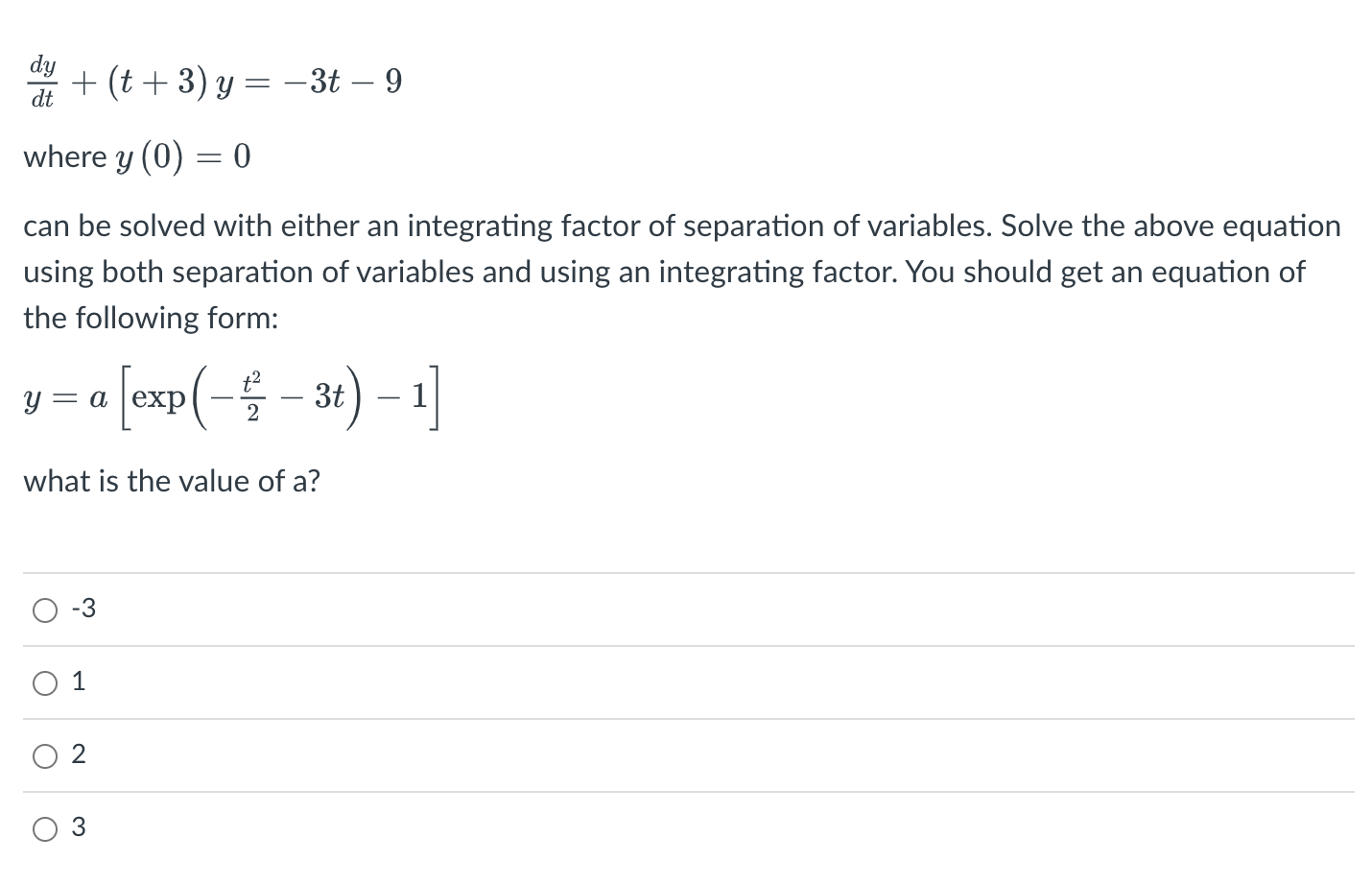
dy at + (t+ 3) y= -3t - 9 where y (0) = 0 can be solved with either an integrating factor of separation of variables. Will both methods produce the same answer? O Yes O Nod df+(t+3)y=3t9 wherey(0) =0 can be solved with either an integrating factor of separation of variables. Solve the above equation using both separation of variables and using an integrating factor. You should get an equation of the following form: y = o; [exp( 3t) 1] what is the value of a? 0-3 01 02 03 The cooling of hot coffee can be described by the following equation: mcp at dT - -hA(T - Troom) where 1. m is the mass of the coffee (in SI units, kg) 2. Cp is the heat capacity of the coffee (in SI units, J/(kg . C) 3. T is the temperature of the coffee (in SI units, C) 4. Troom is the temperature of the room (in SI units, C) 5. h is the heat transfer coefficient (in SI units, W/(m2 .C) 6. A is the surface area of the cup (in SI units, m2) 7. t is time (in SI units, s) If room temperature is 25 . C and the coffee is originally at 80 C, how long will it take the coffee to cool to 45 .C if the ratio hA = 3 x 10 4s 1? Provide your answer in minutes. O 0.56 minutes 5.6 minutes 56 minutes 560 minutes