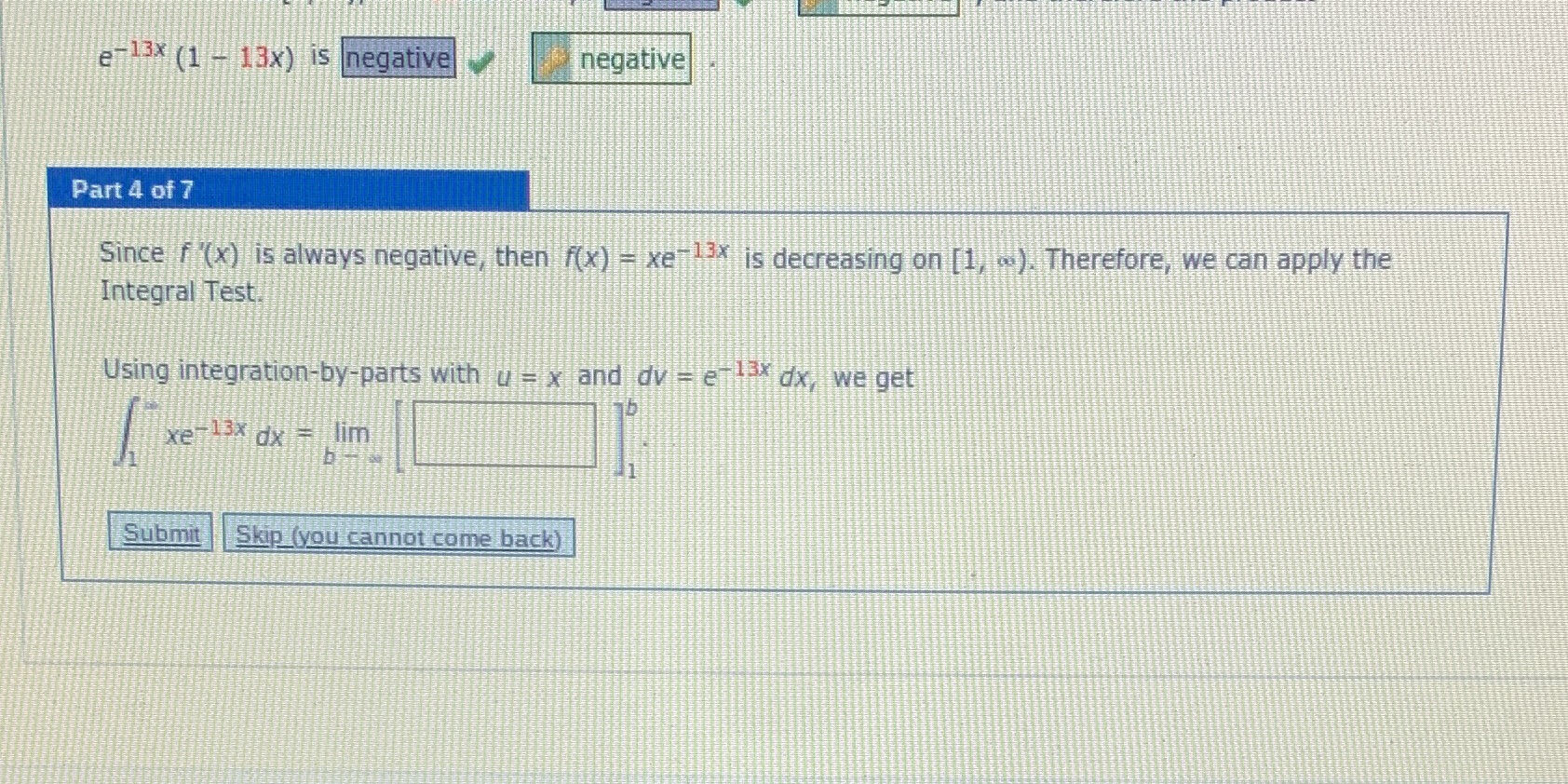
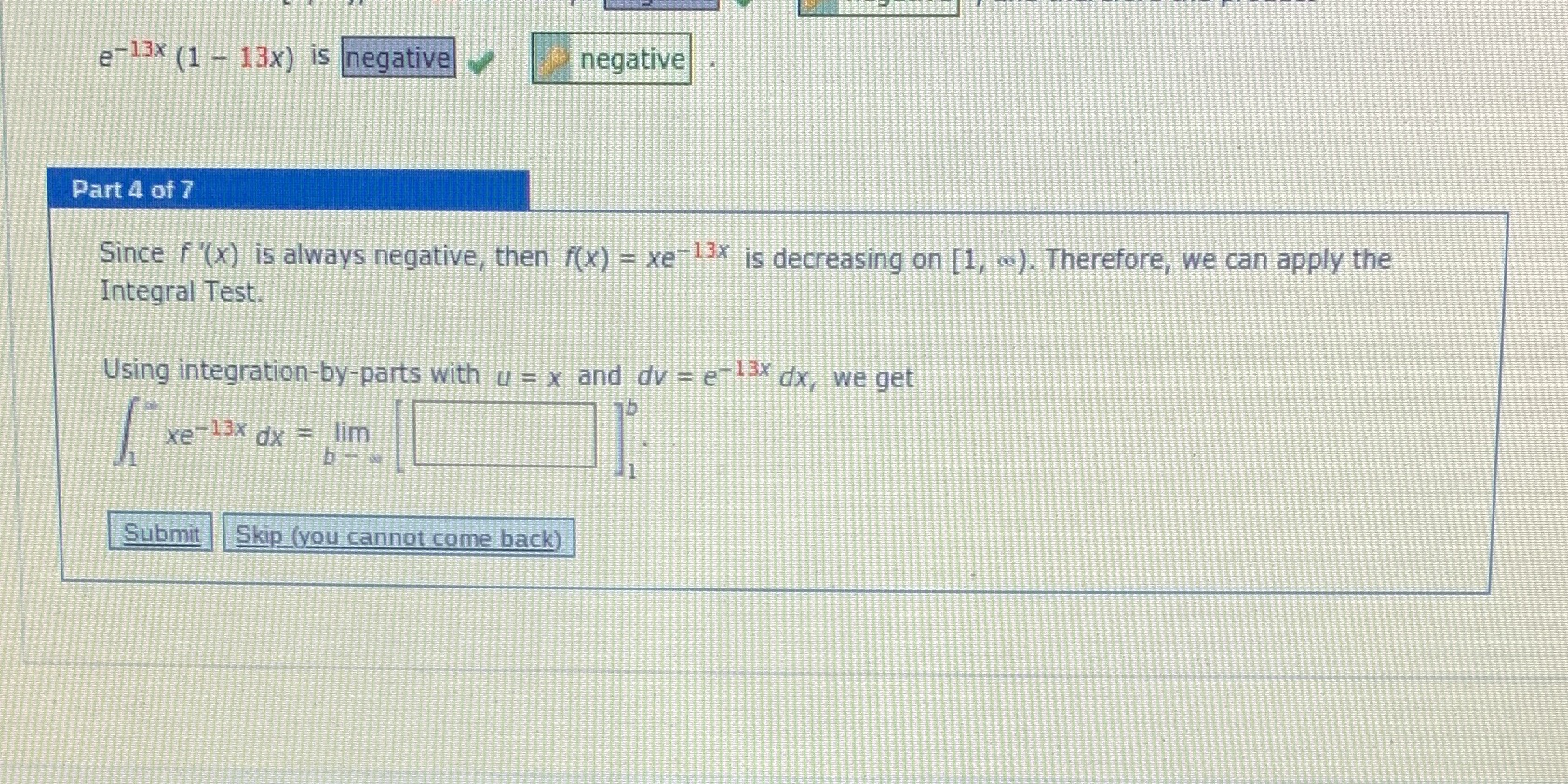
e 13x (1 - 13x) is negative negative Part 4 of 7 Since f '(x) is always negative, then f(x) - xerox is decreasing on [1) .>). Therefore, we can apply the Integral Test. Using integration-by-parts with u = x and dv = enti dx, we get xerox dx = lim b- Submit Skip (you cannot come back)