each step should be solved separately and accourdingly the question requirements, Thanks

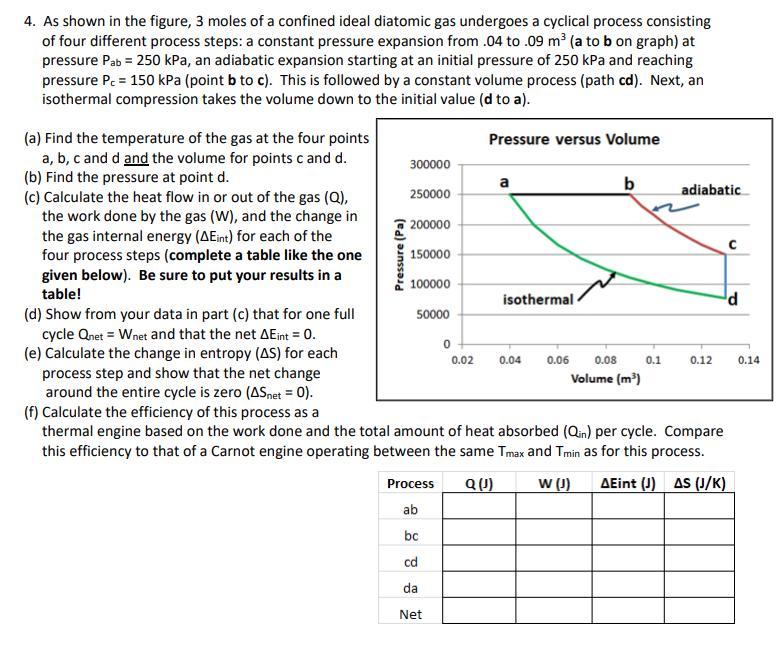
4. As shown in the figure, 3 moles of a confined ideal diatomic gas undergoes a cyclical process consisting of four different process steps: a constant pressure expansion from .04 to .09 m (a to b on graph) at pressure Pab = 250 kPa, an adiabatic expansion starting at an initial pressure of 250 kPa and reaching pressure Pc = 150 kPa (point b to c). This is followed by a constant volume process (path cd). Next, an isothermal compression takes the volume down to the initial value (d to a). Pressure (Pa) (a) Find the temperature of the gas at the four points Pressure versus Volume a, b, c and d and the volume for points c and d. 300000 (b) Find the pressure at point d. 250000 b (c) Calculate the heat flow in or out of the gas (Q), adiabatic the work done by the gas (w), and the change in 200000 the gas internal energy (AEint) for each of the four process steps (complete a table like the one 150000 given below). Be sure to put your results in a 100000 table! isothermal d (d) Show from your data in part (c) that for one full 50000 cycle Qnet = Wnet and that the net AEint = 0. (e) Calculate the change in entropy (AS) for each 0.06 process step and show that the net change Volume (m) around the entire cycle is zero (ASnet = 0). (f) Calculate the efficiency of this process as a thermal engine based on the work done and the total amount of heat absorbed (Qin) per cycle. Compare this efficiency to that of a Carnot engine operating between the same Tmax and Tmin as for this process. Process Q(1) w() AEint (1) AS (J/K) ab 0 0.02 0.04 0.08 0.1 0.12 0.14 bc cd da Net