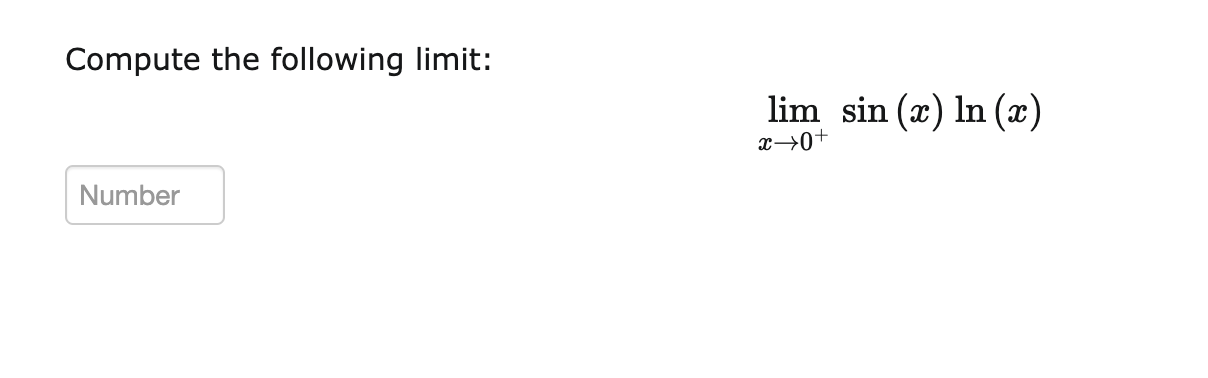
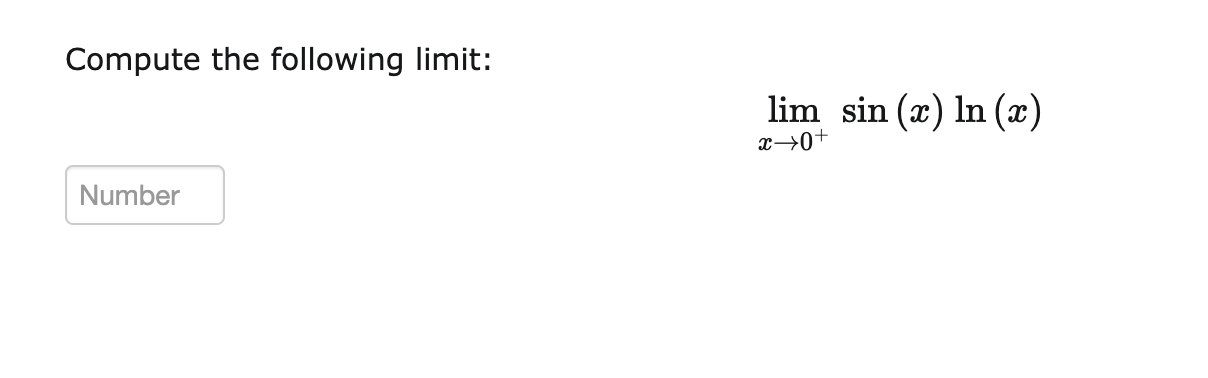
ed -1 Evaluate limFind the limit: lim sin (4x) x-+0 sin (6x)\fEvaluate lim ( 1 In(ac + 1)A commonly used model of the behaviour of atoms in a lattice (i.e., a solid) at low temperatures (developed by Einstein) implies that the heat capacity, 0, per atom in the solid as a function of temperature, T, (in kelvin) is given by E cm = lacs) e- where k and E are constants (specically Boltzmann's constant and one \"quanta" of energy respectively). Let's investigate what happens to this heat capacity as the temperature approaches absolute zero. (a) We would like to compute lim C(T), but this is pretty messy, so let's first make the substitution :1: = i T>0+ 1:1\" and rewrite C as a function of 11:. C(m) = E (b) With this substitution in place, where should we take the limit? In other words, given that we started with T > 0+, what should we have :3 approach? 3) .B (c) Evaluate this limit (L'Hopital's Rule should come in handy.). lim C(T) = 1imC(:l:) = Number T>0+ 1)? (d) True or false: This model agrees with the Third Law of Thermodynamics which requires the heat capacity of any system to go to zero at a temperature of absolute zero? 0 True 0 False