Question: Let G be a set defined as follows: if z is a propositional variable, then z G: if f1, f2 G, then f G.

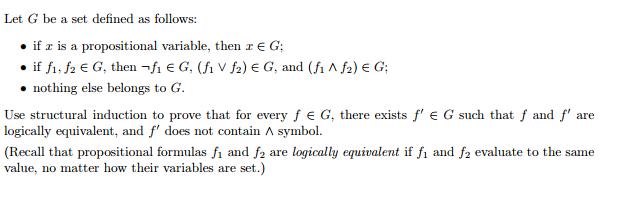
Let G be a set defined as follows: if z is a

Let G be a set defined as follows: if z is a propositional variable, then z G: if f1, f2 G, then f G. (fi V f2) G. and (f ^ f2) = G; nothing else belongs to G. Use structural induction to prove that for every f G, there exists f' G such that f and f' are logically equivalent, and f' does not contain a symbol. (Recall that propositional formulas fi and f2 are logically equivalent if fi and f2 evaluate to the same value, no matter how their variables are set.)

Step by Step Solution

★★★★★

3.43 Rating (166 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

2 3 a propoxional variable done Now f f2 G 71 G fi V f E G fi Af 7 7 f V 7 f x Jo is 1 1 fv 7f ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (2 attachments)

635daca76cf4f_177887.pdf

180 KBs PDF File

635daca76cf4f_177887.docx

120 KBs Word File

Students Have Also Explored These Related Accounting Questions!

Calculate gross profit, cost of goods sold, and selling price MBI, Inc., hat sales of $250 million for fiscal 2013. The company's gross profit ratio for that year was 37.2%,

Inventory turnover is calculated as cost of goods sold divided by ending inventory . 1. True 2. False

Suppose you are buying a car of $26000. The dealer offers that you pay a down payment of $4000 now. Then you will pay the balance with equal monthly payments for 42 months with 6% APR compounded...

Let T be a binary tree with n positions that is realized with an array representation A , and let f () be the level numbering function of the positions of T , as given in Section 8.3.2. Give...

Explain informally the difference between Godel's completeness theorem and his first incompleteness theorem. [8 marks] (b) State the meaning of Hoare triples {P} C {Q} in separation logic. [3 marks]...

Suppose that f is a differentiable function. (a) Find d/dx f(f(x)). (b) Find d/dx f(f(x))). (c) Let f|n| denote the function defined as follows: f|1| = f and f[n] = f f[n-1] for n 2. Thus f|2| = f ...

Let (a, b). The set of strings of elements of of arbitrary length is called a "dictionary" based on the "alphabet" E. Let B and C be defined as follows: B = {WE : length(w) 2) , C (w E . : length(W2...

Project requires code to be executable. Base Code is included at the bottom for your convenience. Code in C++. Base Code for your convenience: You will write an nxn tic-tac-toe game/program that...

Let S be the set of binary strings defined recursively as follows: Basis step: 1 elementof S Recursive step: If x elementof S then xx elementof S and 0r0 elementof S (If x and y are binary strings...

6. Structural Induction (15 points) Let S be a subset of the set of integers defined recursively as follows: Base case: (0,0) E S Recursive case: If (a, b) E S then (a +1,b+2) S. 1) List the elements...

Find the court decision located at 133 T. C. No. 8. a. Which court heard the case? b. Who was the judge(s)? c. In what year was the case decided? d. What was the issue(s) involved?

Problem 2 [4 marks] A steel pipe has a fluid flowing through it at 100C, resulting in a convective heat transfer coeffi- cient of 200 W m2 K-. The steel pipe is surrounded by a very thin heater...

Two community organizations are forming relationships that will help both organizations in capacity building. This most closely describes which of the following? (p. 291) Question 10Answer a....

On January 1, 2015, Tropical Paradise borrows $50,000 by agreeing to a 6%, six-year note with the bank. The funds will be used to purchase a new BMW convertible for use in promoting resort properties...

Jack Corporation paid $380,000 for 40 percent of Jill Corporations outstanding voting common stock on July 1, 2011. Jills stockholders equity on January 1, 2011, was $500,000, consisting of $300,000...

Let n1 = 100, X1 = 50, n2 = 100, and X2 = 30. a. At the 0.05 level of significance, is there evidence of a significant difference between the two population proportions? b. Construct a 95% confidence...

Textile Company frequently factors its accounts receivable. During 2007, Faeber made credit sales of $100,000 to customers, under terms of 2/10, n/30. Faeber records its credit sales using the gross...

Arb Corporation acquired 25 percent of Tee Corporation's outstanding common stock on October 1, for $600,000. A summary of Tee's adjusted trial balances on this date and at December 31 follows (in...

What is a target market? Why do most start-ups focus on relatively small target markets to being with?

Let r and s be solutions to the quadratic equation x 2 b x + c = 0. For n N, define d0 = 0 d1 = r s dn = b dn1 c dn2 (n 2) Prove that dn = r n s n for all n N. [4 marks] (b) Recall that a commutative...

Given a flow network G = (V, E), let f1 and f2 be functions from V V to R. The flow sum f1 + f2 is the function from V V to R defined by (26.4) (fi + f2) (u, v) = f1 (u, v) + f2(u, v) for all u, v ...

I need help with Exercise #3 pleas use the attached materials only to solve the problem. thank you Section 3B Limits of Integrals & Integrals of Limits 93 Case 1: Suppose y (X) 0. By 3.28, there...

Describe, in detail, how the heapsort algorithm works. [10 marks] Show that the worst-case cost of heapsort is O(n log n). [6 marks] Would it be possible to implement a variant of heapsort based on a...

SUMMARY this article for about 2 pages with single spacing. Thank you. ECONOMETRICS: MEASUREMENT I N ECONOMICS1 I As the first incumbent of a new Chair in this University, I thought that in this...

ttth Suppose that the sequence of bags {Bn | n N} is recursively enumerated by the computable function e(n, x) = fn(x), [7 marks] Hence prove that the set of all recursive bags cannot be recursively...