Question: Eliminate the parameter t to find a simplified Cartesian equation of the form 3; 2 ma: + b for {$03) = 20 t y(t) =





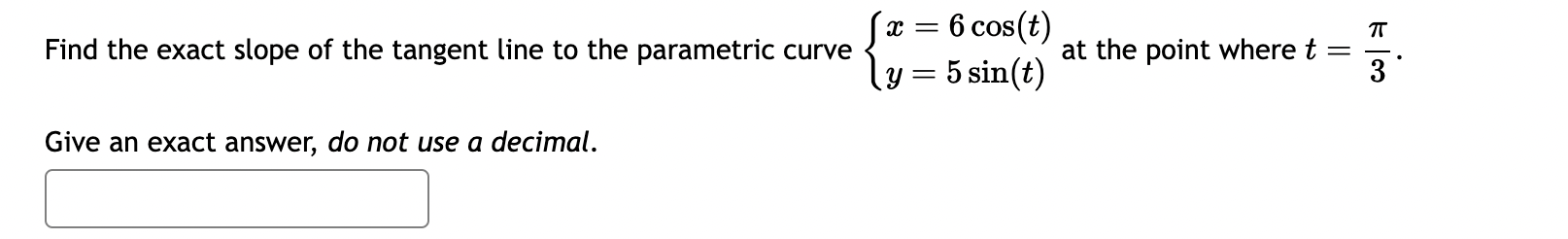






![written as :c = l:] x = 2 cos(t) Find the slope](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66669e4c73b90_22866669e4c5607d.jpg)

Eliminate the parameter t to find a simplified Cartesian equation of the form 3; 2 ma: + b for {$03) = 20 t y(t) = 17 2t Suppose parametric equations for the line segment between (9, 6) and (O, 8) have the form: {$05) 2 61+ bt y(t) = c +dt If the parametric curve starts at (9, 6) when t = 0 and ends at (0, 8) at t = 1, then find a, b, c, and d. \"= b=_ c=_ d=_ The ellipse 62 + 52 = 1 can be drawn with parametric equations where x (t) is written in the form x (t) = r cos(t) with r = and y(t) =Eliminate the parameter t to find a Cartesian equation in the form a: = y) for: {$(t) 2 5t2 y(t) = 8 + 473 The resulting equation can be written as :c = l:] x = 2 cos(t) Find the slope of the tangent line to the parametric curve at the point y = 4 sin(t)x = 6 cos(t) Find the exact slope of the tangent line to the parametric curve at the point where t = y = 5 sin(t) Give an exact answer, do not use a decimal.Next ., , , .. . , m=59+ The posmon of an ObJECt at time t is given by the parametric equations y=5+1' Find the horizontal velocity, the vertical velocity, and the speed at the moment where t : 1. Do not worry about units in this
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


