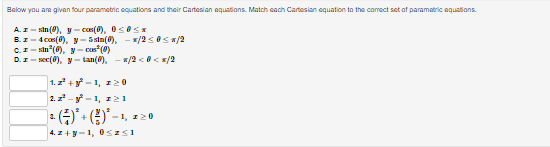
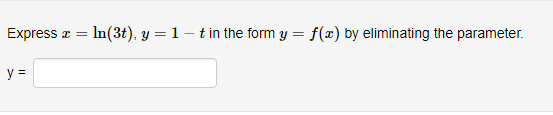
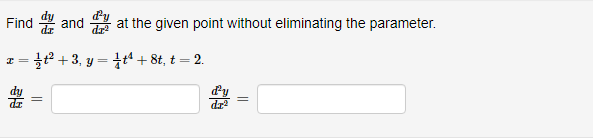
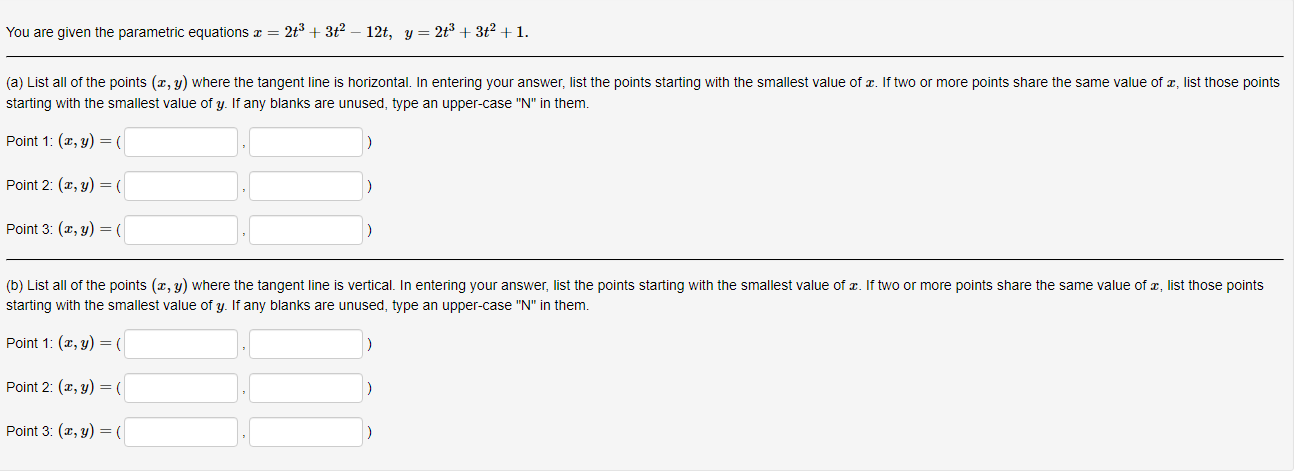
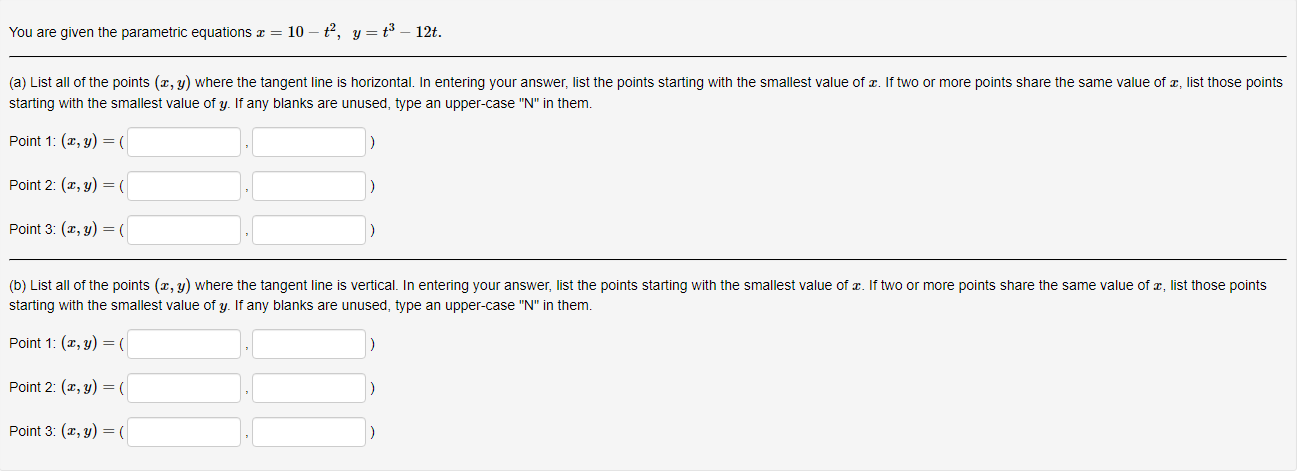
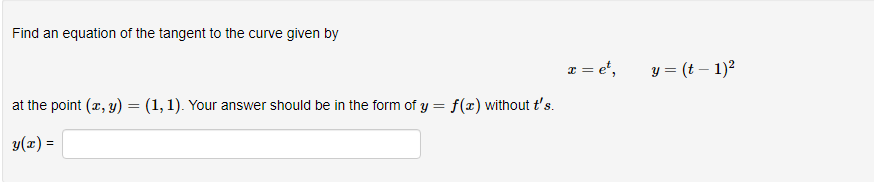
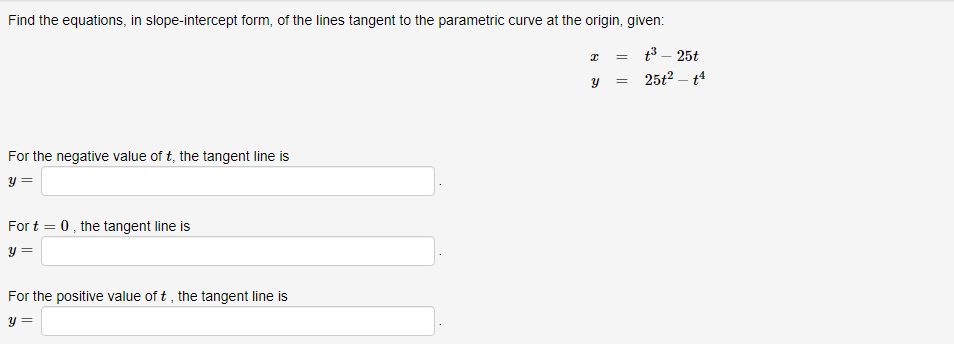
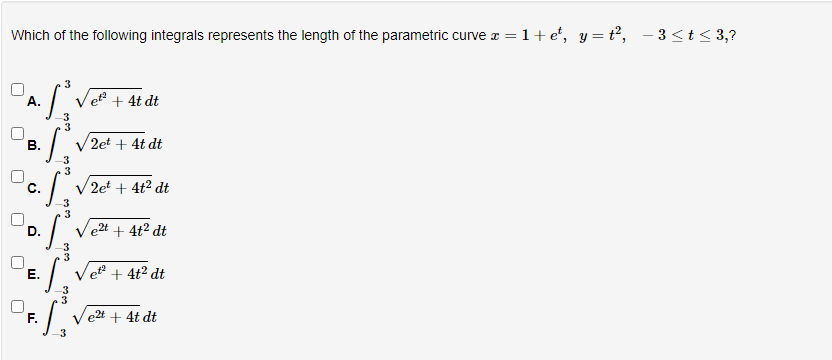
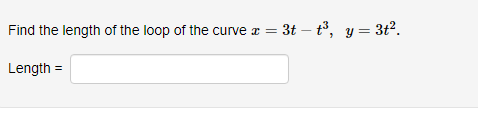
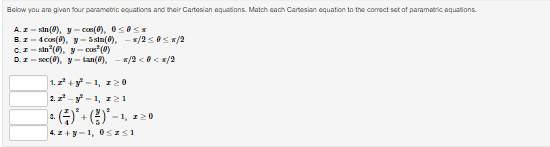
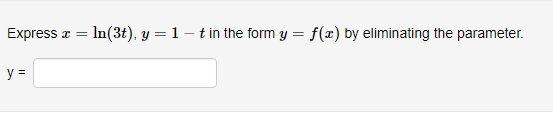
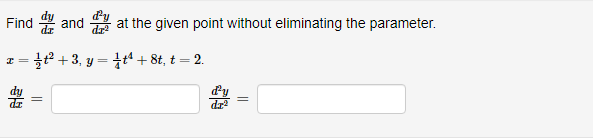
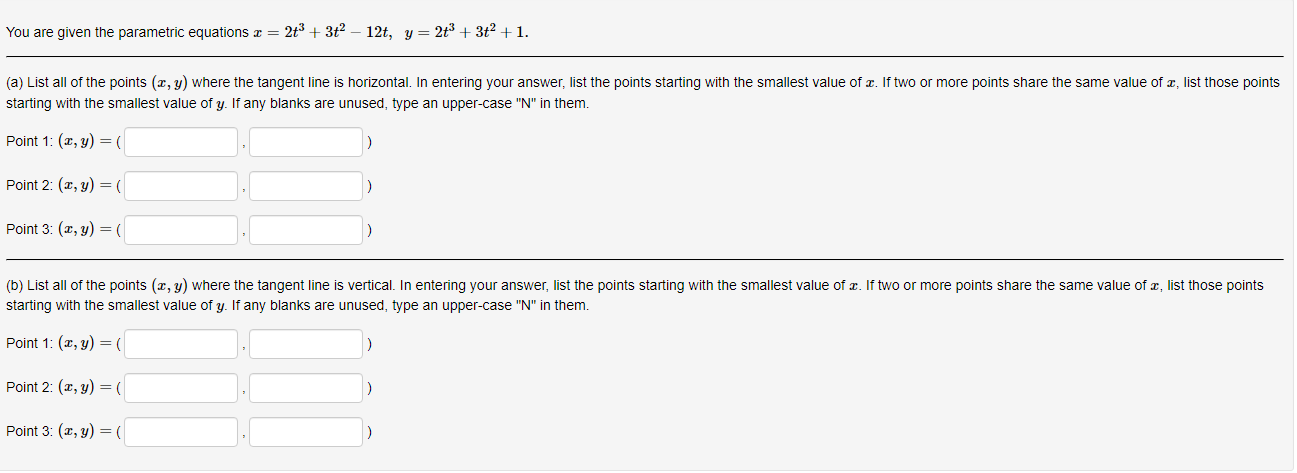
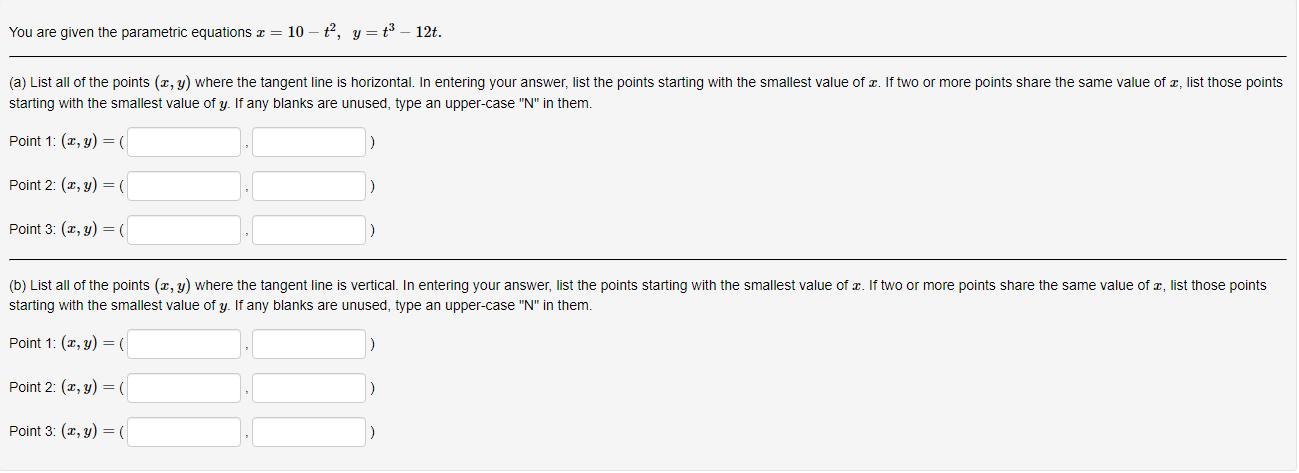
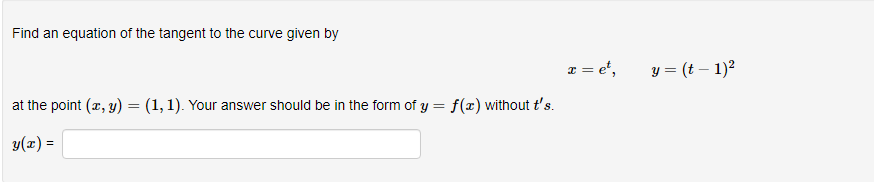
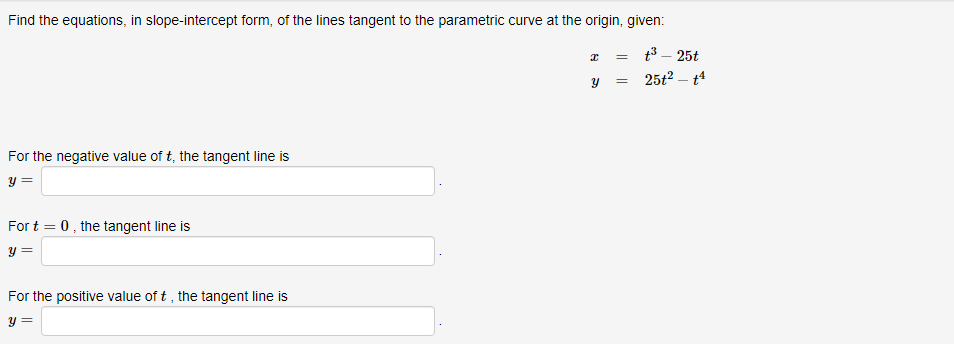
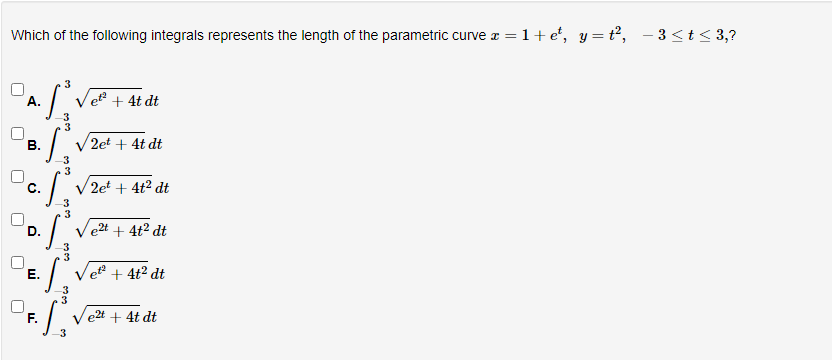
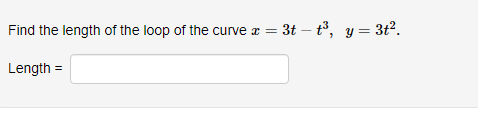
Below you am given four parametric equations and their plots. Match each plot in the correct set A. I - cuss(at), y - sim(at), 15152 B. I - 2 + cos((), y- 3 + an(1), Ost5 2x C. I - 2sin(t), y - 3 cos(t), 05132 D. I - co ((), y - cost), OS15 4x 1 compete ncialon 1 complete setstion Hewas up and down he curve laice 0.5- 0.5- 9 0.5 0.5 -0.5-Each set of parametric equations below describes the path of a particle that moves along the circle I" + (y - 1)2 - 4 in some manner. Match each set of parametric equations to the path that it describes. A. Once around clockwise, starting at (2, 1). B. Three times around counterclockwise, starting at (2, 1). C. Halfway around counterclockwise, starting at [0, 3). 1. 2 -2cus(t), y - 1 4 2sin(1), x/2s ts 3x/2 2. z-2cos(1), y - 1 - 2xin(1), Ost$ 2x 3. z - 2cos(t), y - 14 2xin(1), Oct3 6xThe cide (3 - 0)3 + (y-5)- - 9 can be drawn with parametric equations. Assume the cincin is traced clockwise as the pammater incmazes. than F=Below you am given four parametric equations and their Cartesian aquations. Match each Cartesian equation to the correct set of pammatric equations. As - al(9), y-08(0), 0305x B. I - 408(0), y- 5am(0), -7/2505 w/2 C. I - SIn (0), y cus (9) DI-(0), y -0). -w/206/2 1.xty-1 120 + -1, 120 Axty-1 0gas1Eliminate the parameter to find the cartesian equation of the curve: The equation of the curve is: VE from X = to X= Express c = In(3t), y =1 - t in the form y = f(@) by eliminating the parameter. V=Use calculus to find the exact Cartesian coordinates of the leftmost point on the parametric curve 1=t*- t', y = t+ In(t). (I, y) = (Find an equation for each line that passes through the paint (4' 3) and iS tangentto the parametric curve I=3t2+1, y=2t3+ 1. If there is more than one answer then order your answers consecutively so lines with smaller slopes appear before lines with larger slopes If some answer elds are not used enter None in the unused answer Dian Ks and list them last. Tangent line 1: y = Tangent line 2: y = Tangent line 3: y = Find du d'y and dad at the given point without eliminating the parameter. I= t' +3, y = 4t' + 8t, t = 2. dy d'y = =You are given the parametric equations = = 2t + 3t2 - 12t, y = 2+ + 3t2 + 1. (a) List all of the points (@, y) where the tangent line is horizontal. In entering your answer, list the points starting with the smallest value of c. If two or more points share the same value of a, list those points starting with the smallest value of y. If any blanks are unused, type an upper-case "N" in them. Point 1: (x, y) = ( Point 2: (x, y) = ( Point 3: (x, y) = ( (b) List all of the points (x, y) where the tangent line is vertical. In entering your answer, list the points starting with the smallest value of a. If two or more points share the same value of x, list those points starting with the smallest value of y. If any blanks are unused, type an upper-case "N" in them. Point 1: (x, y) = ( Point 2: (x, y) = ( Point 3: (x, y) = (You are given the parametric equations = = 10 -+, y = t - 12t. (a) List all of the points (@, y) where the tangent line is horizontal. In entering your answer, list the points starting with the smallest value of c. If two or more points share the same value of , list those points starting with the smallest value of y. If any blanks are unused, type an upper-case "N" in them. Point 1: (x, y) = ( Point 2: (x, y) = ( Point 3: (x, y) = ( (b) List all of the points (z, y) where the tangent line is vertical. In entering your answer, list the points starting with the smallest value of . If two or more points share the same value of z, list those points starting with the smallest value of y. If any blanks are unused, type an upper-case "N" in them. Point 1: (x, y) = ( Point 2: (x, y) = ( Point 3: (x, y) = (Find an equation of the tangent to the curve given by y = (t- 1)2 at the point (x, y) = (1, 1). Your answer should be in the form of y = f(x ) without t's. y(x) =Find the equations, in slope-intercept form, of the lines tangent to the parametric curve at the origin, given: I = 1925: zetat4 H: II For the negative value of t: the tangent line is y = Fort = CI = the tangent line is y : For the positive value of t , the tangent line is y = Which of the following integrals represents the length of the parametric curve x = t + cos(t), y = t - sin(t), 0