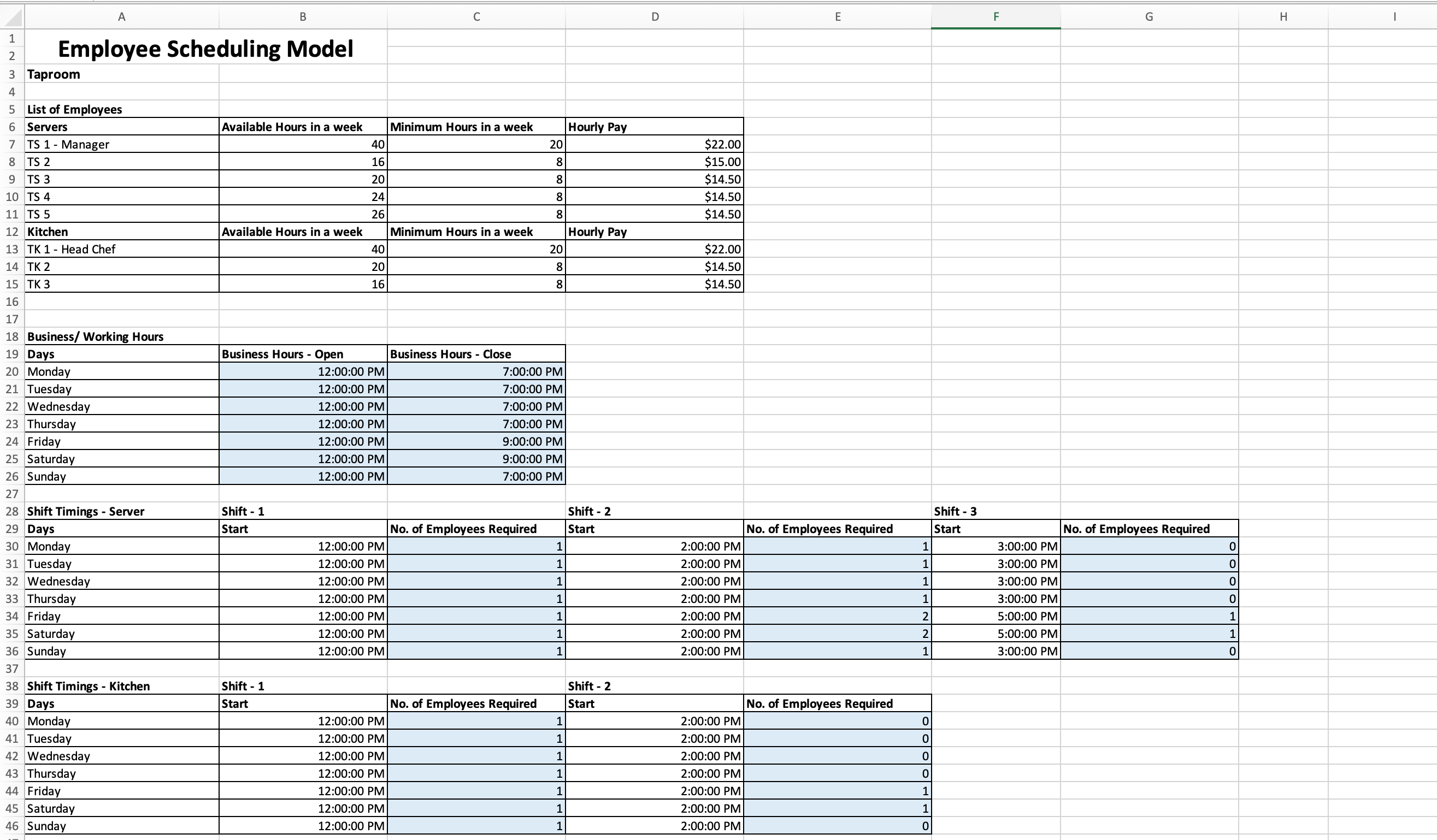
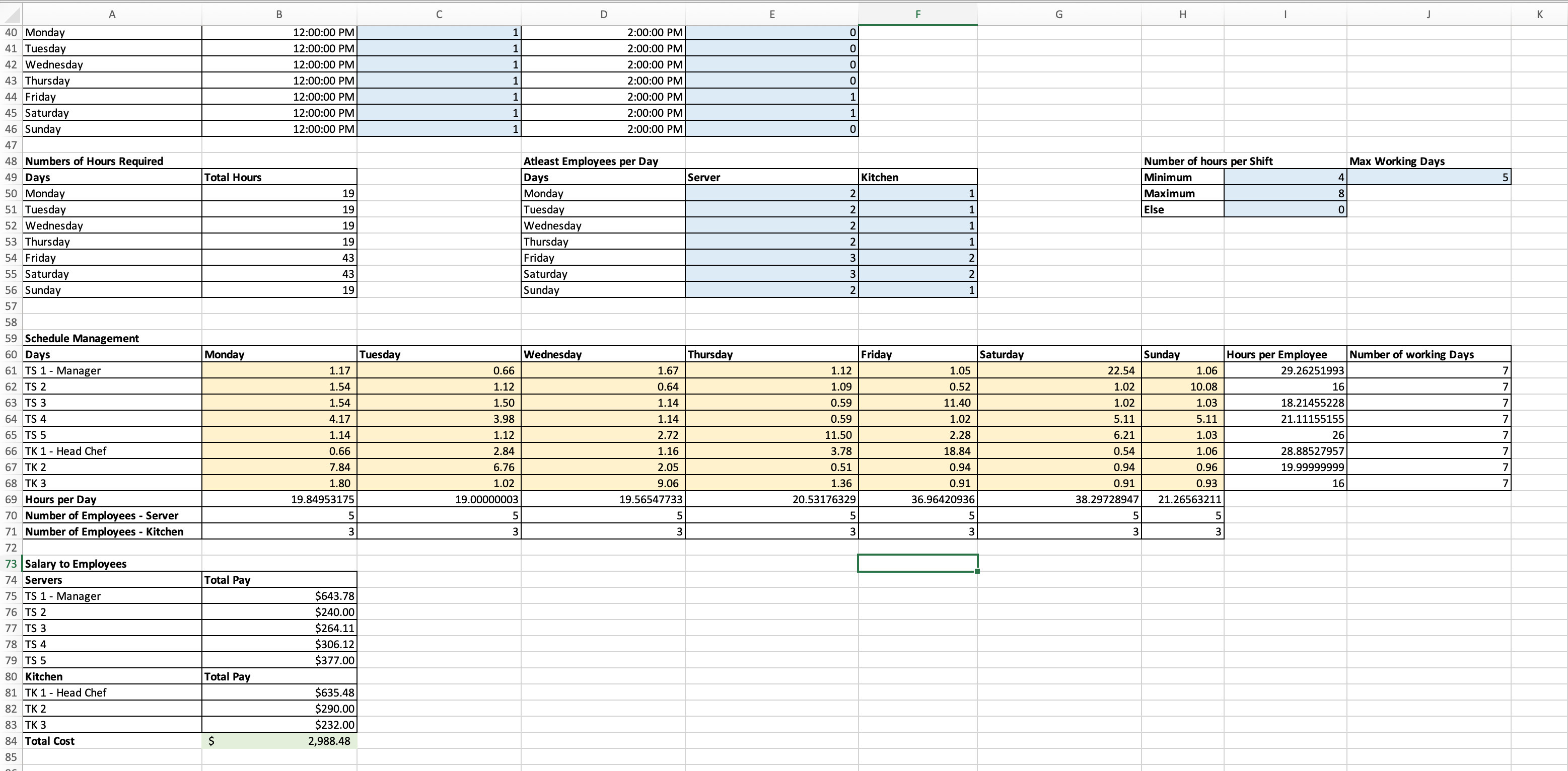
Employee schedule optimization. 8 staff. 5 servers, 3 kitchen staff. Business is open 7 days a week, Sunday-Thursday from 12-7, Friday and Saturday 12-9. They need a minimum of 2 servers per day, 1 kitchen staff per day from Sunday-Thursday. They need a minimum of 3 servers per day, 2 kitchen staff per day on Friday and Saturday. They cannot work more than 5 days in a week. They need to work a minimum of 4 hours per shift.

We are running into an issue with Solver not being able to find a solution that satisfies all our constraints. We have tried changing the constraints but this leads to other issues.

Please fix the issue

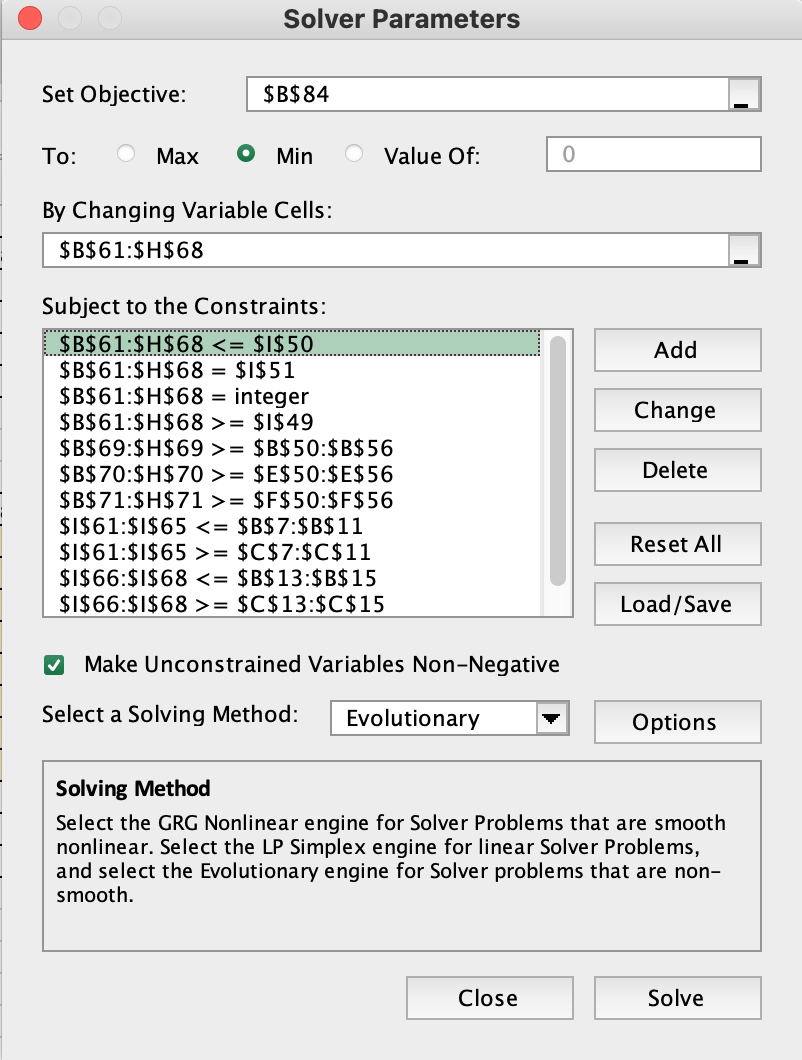
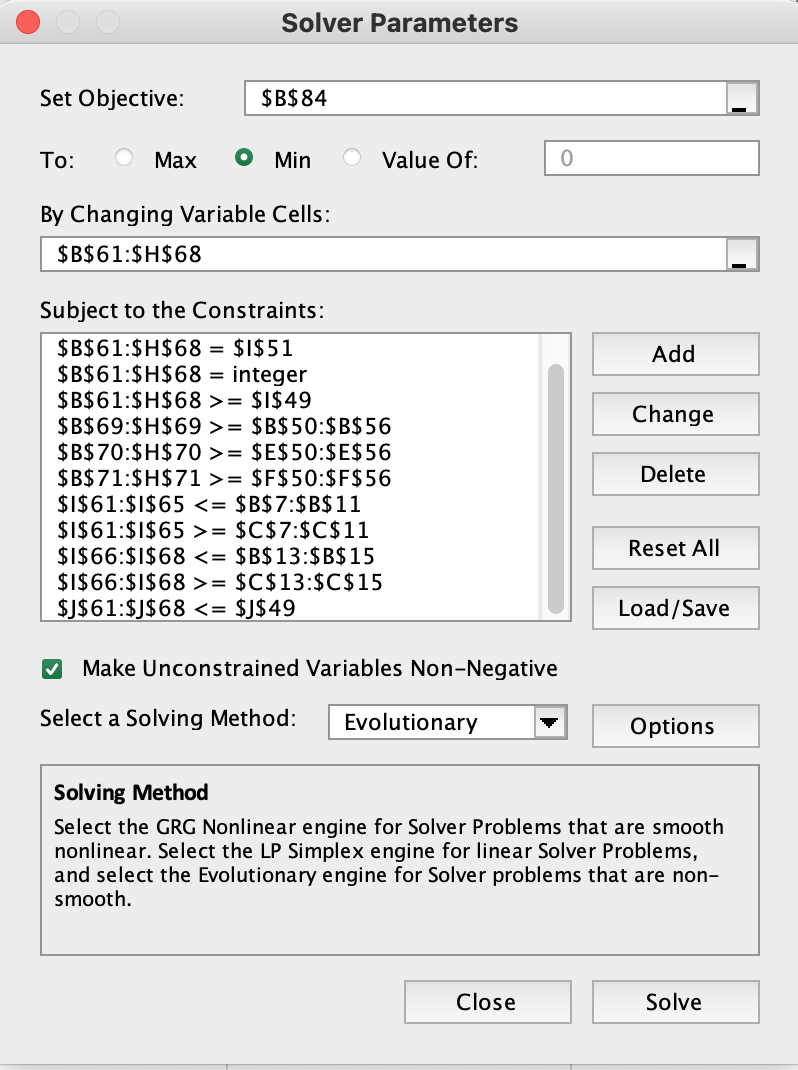
To: - Min Value Of: By Changing Variable Cells: Suhiert to the Conctraints: Make Unconstrained Variables Non-Negative Select a Solving Method: Solving Method Select the GRG Nonlinear engine for Solver Problems that are smooth nonlinear. Select the LP Simplex engine for linear Solver Problems, and select the Evolutionary engine for Solver problems that are nonsmooth. By Changing Variable Cells: Subject to the Constraints: $B$61:$H$68=$1$51$B$61:$H$68=integer$B$61:$H$68>=$1$49$B$69:$H$69>=$B$50:$B$56$B$70:$H$70>=$E$50:$E$56$B$71:$H$71>=$F$50:$F$56$1$61:$1$65=$C$7:$C$11$1$66:$1$68=$C$13:$C$15$J$61:$J$68=$1$49$B$69:$H$69>=$B$50:$B$56$B$70:$H$70>=$E$50:$E$56$B$71:$H$71>=$F$50:$F$56$1$61:$1$65=$C$7:$C$11$1$66:$1$68=$C$13:$C$15$J$61:$J$68