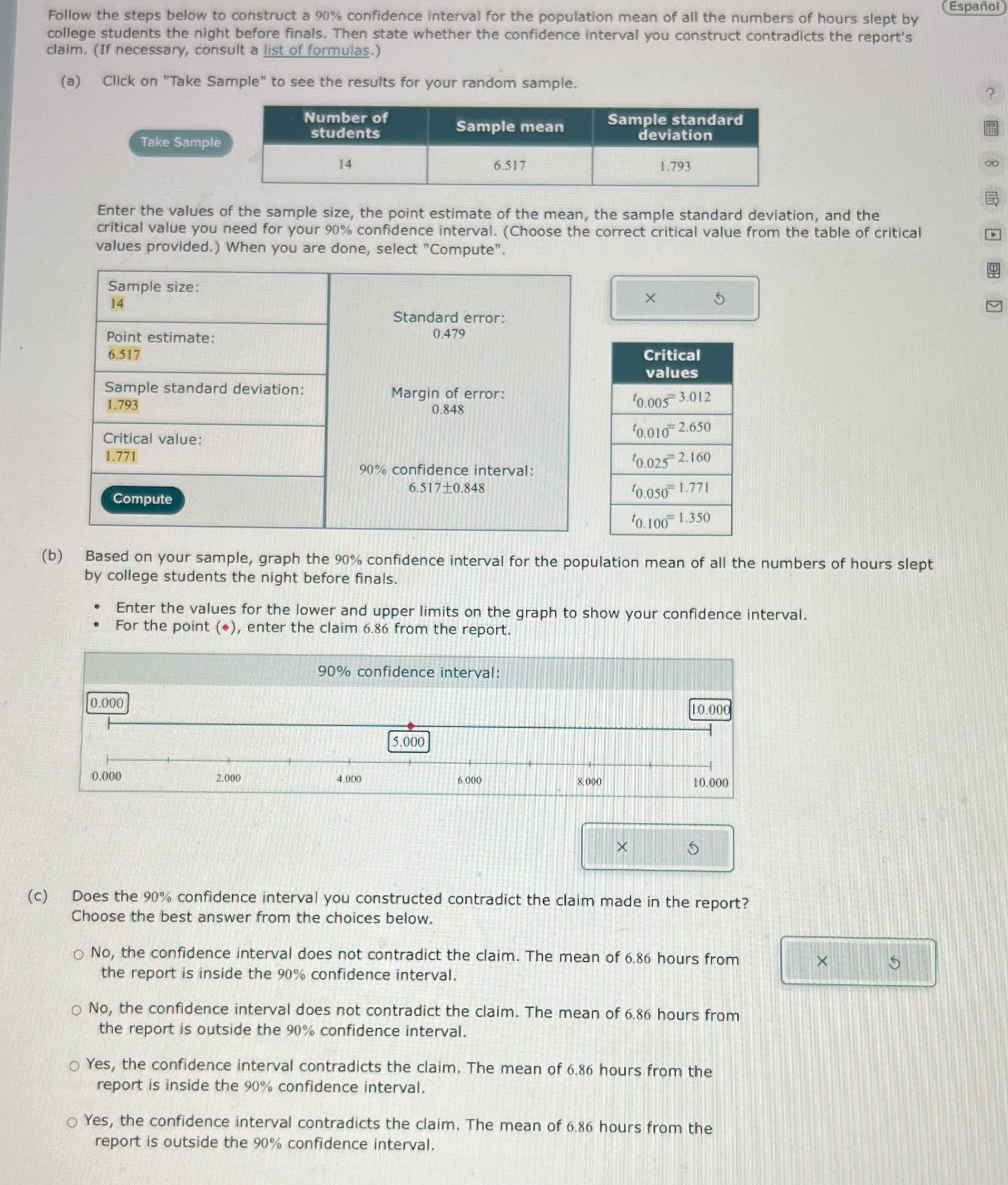
(Esparion) Follow the steps below to construct a 90% confidence interval for the population mean of all the numbers of hours slept by college students the night before finals. Then state whether the confidence interval you construct contradicts the report's 'claim. (If necessary, consult a list of formulas.) (a) Click on "Take Sample\" to see the results for your random sample. (b) () Sample standard Number of students sk Ll deviation Enter the values of the sample size, the point estimate of the mean, the sample standard deviation, and the critical value you need for your 90% confidence interval. (Choose the correct critical value from the table of critical values provided.) When you are done, select "Compute\". Take Sample Standard error: 0479 Sample size: 14 Point estimate: 6.517 Sample standard deviation: 1.793 Critical value: 1.771 10.050" 1.771 Based on your sample, graph the 90% confidence interval for the population mean of all the numbers of hours slept by college students the night before finals. Critical values "0.025 2.160 Margin of error: 0.848 90% confidence interval: 6.51710.848 = Enter the values for the lower and upper limits on the graph to show your confidence interval. * For the point (), enter the claim 6.86 from the report. 90% confidence interval: Does the 90% confidence interval you constructed contradict the claim made in the report? Choose the best answer from the choices below. O No, the confidence interval does not contradict the claim. The mean of 6.86 hours from the report is inside the 90% confidence interval. O No, the confidence interval does not contradict the claim. The mean of 6.86 hours from the report is outside the 90% confidence interval. O Yes, the confidence interval contradicts the claim. The mean of 6.86 hours from the report is inside the 90% confidence interval. O Yes, the confidence interval contradicts the claim. The mean of 6 86 hours from the report is outside the 90% confidence interval, R B & 8 B