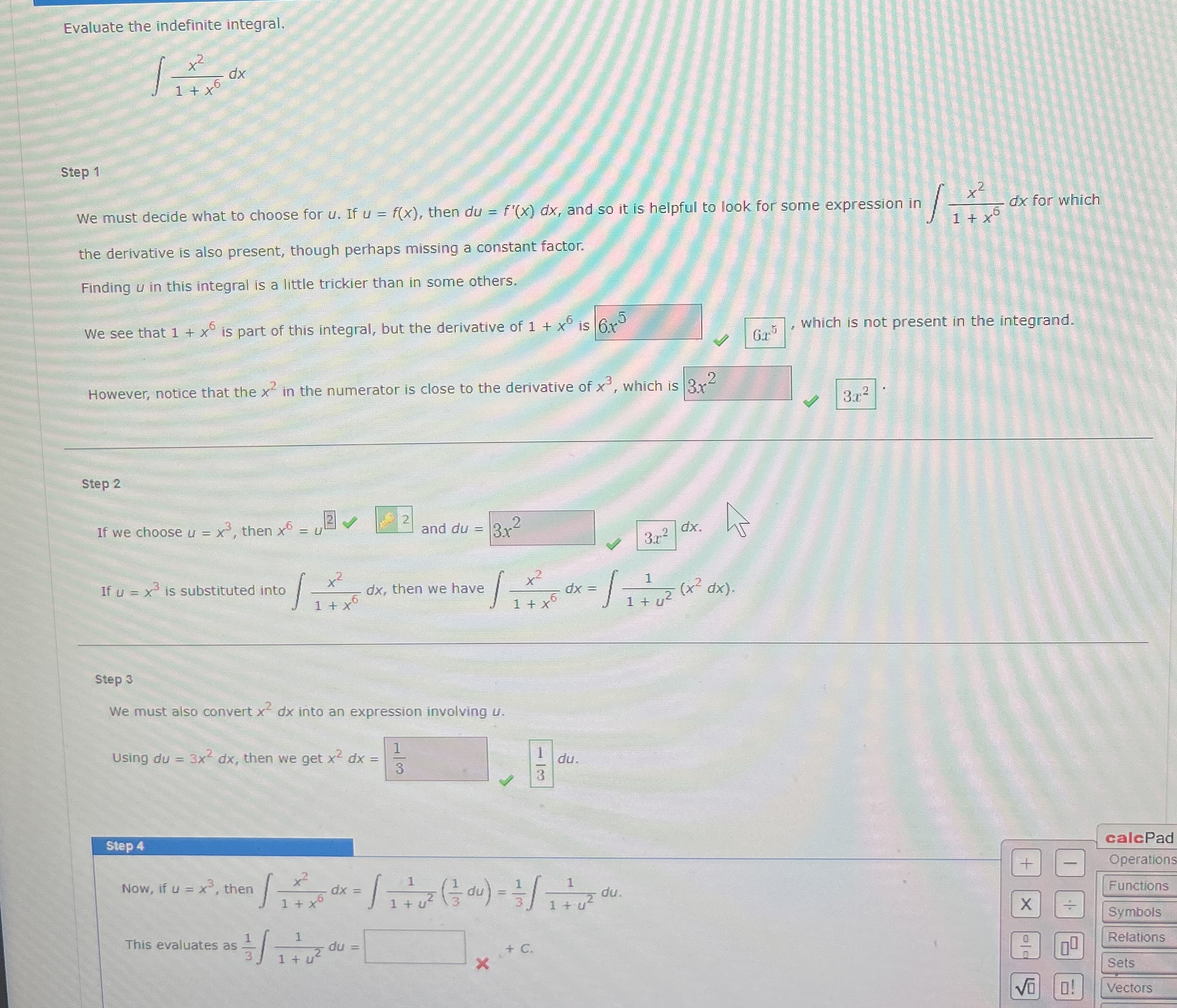
Evaluate the indefinite integral.

${\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}\frac{x^2}{1+x^6}dx$

Step $1$

We must decide what to choose for $u.$ If $u=f(x),$ then $du=f^{\text{'}}(x)dx,$ and so it is helpful to look for some expression in ${\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}\frac{x^2}{1+x^6}dx$ for which the derivative is also present, though perhaps missing a constant factor.

Finding $u$ in this integral is a little trickier than in some others.

We see that $1+x^6$ is part of this integral, but the deriwative of $1+x^6$ is $66x^5$

$$ which is not present in the integrand.

However, notice that the $x^2$ in the numerator is close to the derivative of $x^3,$ which is $3x^2.$

$$

Step $2$

If we choose $u=x^3,$ then $x^6=u2$

$$ and $du=$

$dx$ n

If $u=x^3$ is substituted into ${\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}\frac{x^2}{1+x^6}dx,$ then we have ${\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}\frac{x^2}{1+x^6}dx={\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}\frac{1}{1+u^2}(x^{2}dx)$

$q,$

Step $3$

We must also convert $x^{2}dx$ into an expression involving $u.$

Using $du=3x^{2}dx,$ then we get $x^{2}dx=\frac{1}{3}du.$

Step $4$

Now, if $u=x^3,$ then ${\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}\frac{x^2}{1+x^6}dx={\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}\frac{1}{1+u^2}(\frac{1}{3}du)=\frac{1}{3}{\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}\frac{1}{1+u^2}du.$

This evaluates as $\frac{1}{3}{\displaystyle \underset{\phantom{}}{\overset{\phantom{}}{}}}\frac{1}{1+u^2}du=+c{x}^{+}.$

calcPad

Operations

Functions

Symbols

Relations

Sets

Vectors