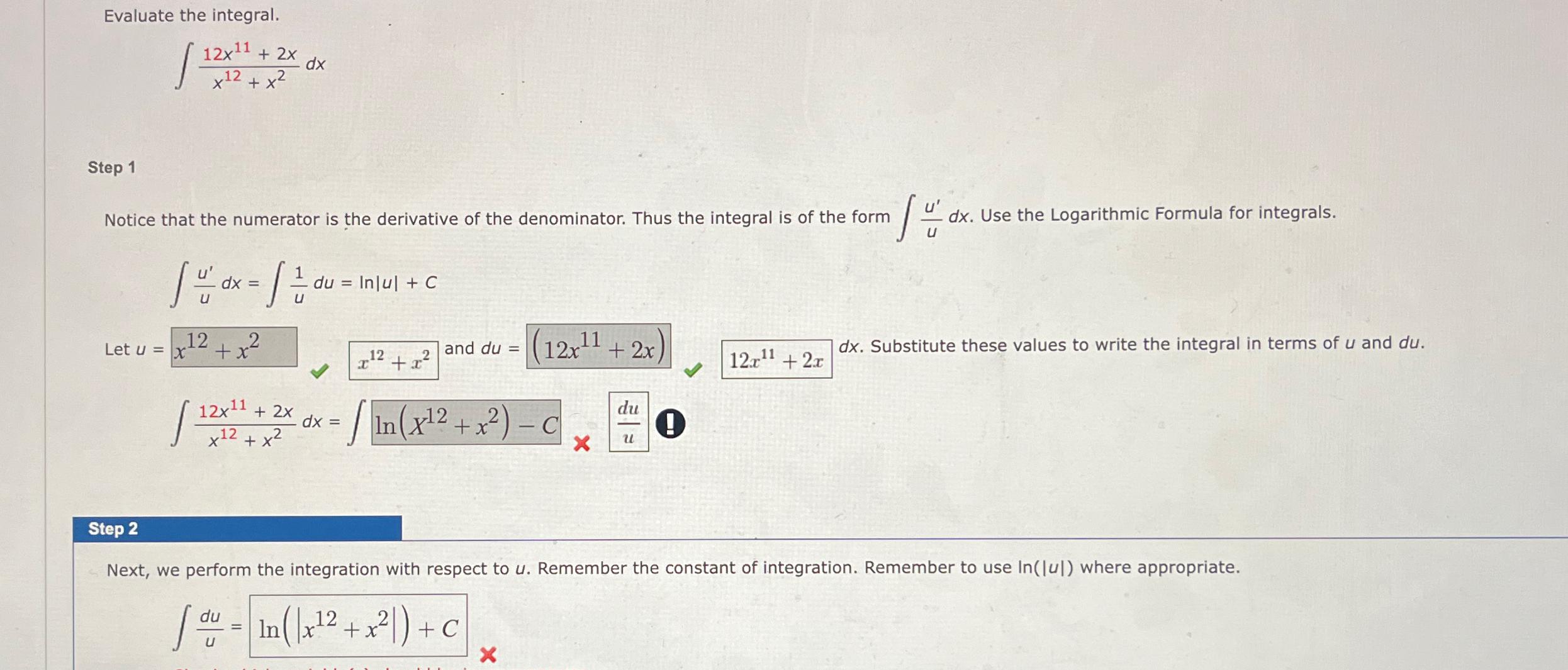
Evaluate the integral. 12x11 + 2x x12 + x / 12X dx Step 1 Notice that the numerator is the derivative of the denominator. Thus the integral is of the form du = Inlu + C Su dx = du U Let u=x dx. dx. Use the Logarithmic Formula for integrals. 12 +x 12 and du = 2 (12x11 +2x) 11 12x+2x dx. Substitute these values to write the integral in terms of u and du. 12x11 + 2x x12 + x2 dx = 1/+12 / In (x 12 + x) - C 2 du Step 2 Next, we perform the integration with respect to u. Remember the constant of integration. Remember to use In([u]) where appropriate. = U In(|x12 + x|) + + C