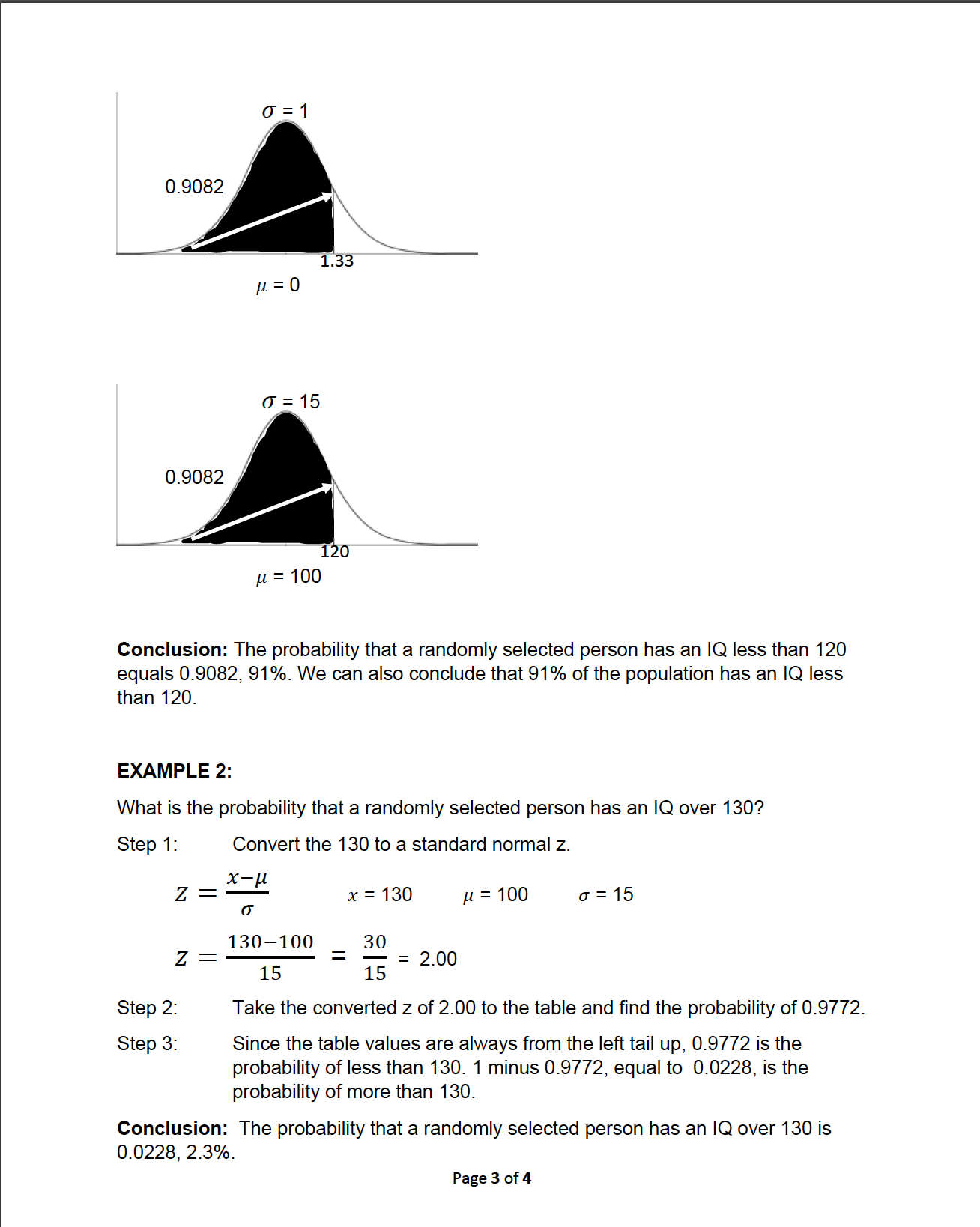
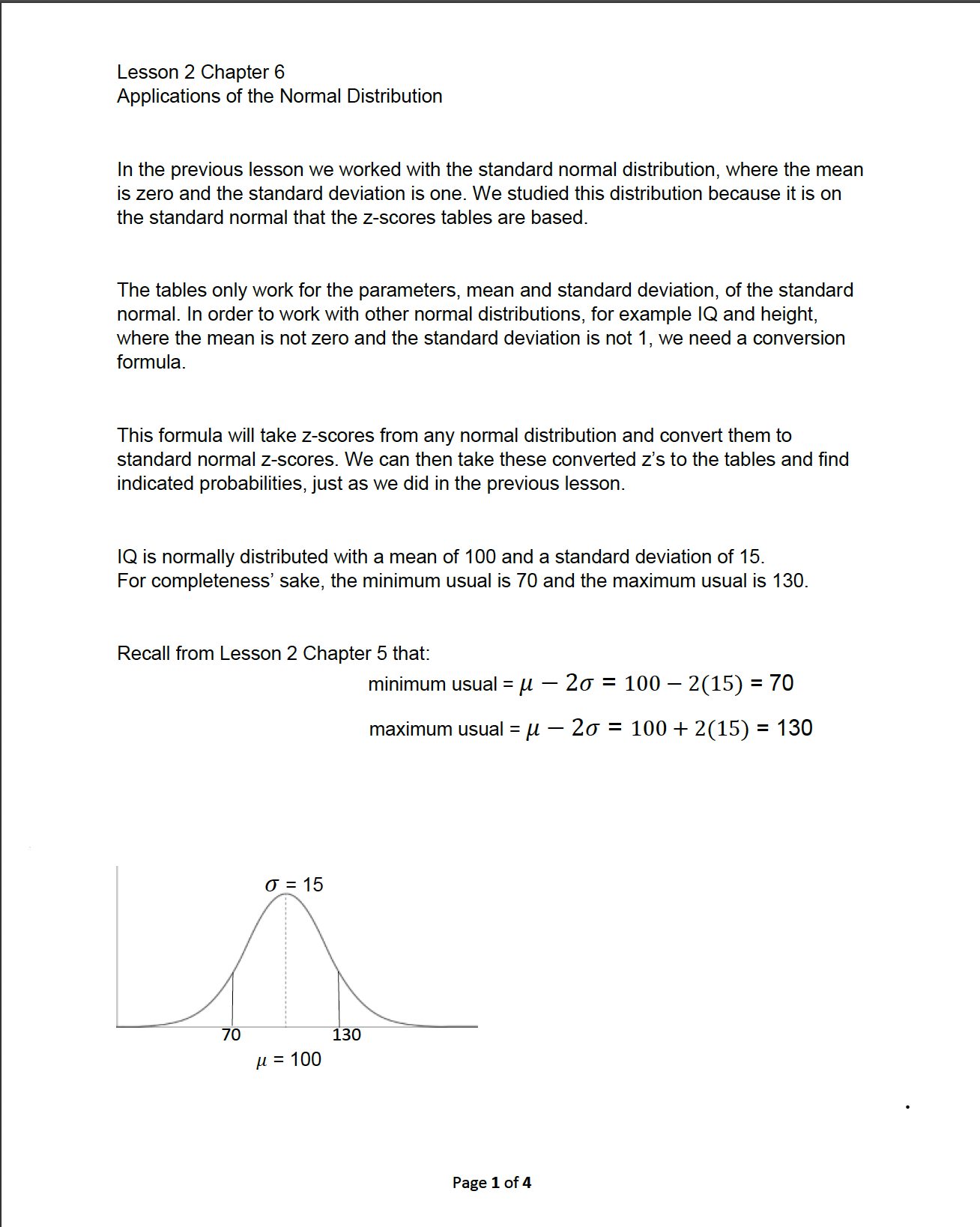
EXAMPLE 1: Let's nd the probability that a randomly selected person has an IQ less than 120. IQ scores have a mean of 100 and a standard deviation of 15. The z-scores tables only work for the standard normal, where the mean is zero and the standard deviation is one. We must take our 2 of 120 and convert it to a standard normal 2. This is the formula we use to convert any z-score to a standard normal zscore. The required standard normal 2 equals the score we want to convert (x) minus the mean (,u) and then divided by the standard deviation (0). For this example, we want to convert 120 to a standard normal 2. x=120 #:100 6:15 _ 120100 20 Z_TE:1'33 The z of 120 in the normal distribution for IQ, converts to a standard normal 2 of 1.33. Now we take the 1.33 to the positive 2 table, as we did in the previous lesson. 1.33 leads to an area (probability) of 0.9082. Page 2 of 4 Conclusion: The probability that a randomly selected person has an IQ less than 120 equals 0.9082, 91%. We can also conclude that 91% of the population has an IQ less than 120. EXAMPLE 2: What is the probability that a randomly selected person has an IQ over 130? Step 1: Convert the 130 to a standard normal 2. x_lu Z= x=130 #:100 6:15 0' Z _ 130100 _ 30 2 00 _ 15 15 _ ' Step 2: Take the converted z of 2.00 to the table and find the probability of 0.9772. Step 3: Since the table values are always from the left tail up, 0.9772 is the probability of less than 130. 1 minus 0.9772, equal to 0.0228, is the probability of more than 130. Conclusion: The probability that a randomly selected person has an IQ over 130 is 0.0228, 2.3%. Page 3 of 4 Lesson 2 Chapter 6 Applications of the Normal Distribution In the previous lesson we worked with the standard normal distribution, where the mean is zero and the standard deviation is one. We studied this distribution because it is on the standard normal that the z-scores tables are based. The tables only work for the parameters, mean and standard deviation, of the standard normal. In order to work with other normal distributions, for example IQ and height, where the mean is not zero and the standard deviation is not 1, we need a conversion formula. This formula will take z-scores from any normal distribution and convert them to standard normal z-scores. We can then take these converted z's to the tables and nd indicated probabilities, just as we did in the previous lesson. IQ is normally distributed with a mean of 100 and a standard deviation of 15. For completeness' sake, the minimum usual is 7'0 and the maximum usual is 130. Recall from Lesson 2 Chapter 5 that: minimum usual = pt 20 = 100 2(15) = 70 maximum usual = 20 = 100 + 2(15) = 130 Page 1 of 4 As always, show your work. IQ scores are normally distributed with a mean of 100 and a standard deviation of 15. 1) What is the probability that a randomly selected person has an IQ of less than 90? 2) What is the probability that a randomly selected person has an IQ of more than 110? The heights of men are normally distributed with a mean of 68.6 inches and a standard deviation of 2.8 inches. 3) What percent of men are less than 5 feet, 6 inches tall? The lengths of pregnancies are normally distributed with a mean of 268 days and a standard deviation of 15 days. 4) Find the probability of a pregnancy lasting more than 280 days. Bonus: What is the probability of a having an IQ between 110 and 120