Example 12 Discuss the continuity of the function defined by x+2, if x <0 f(x) -x+2, if x>0 Solution Observe that the function is

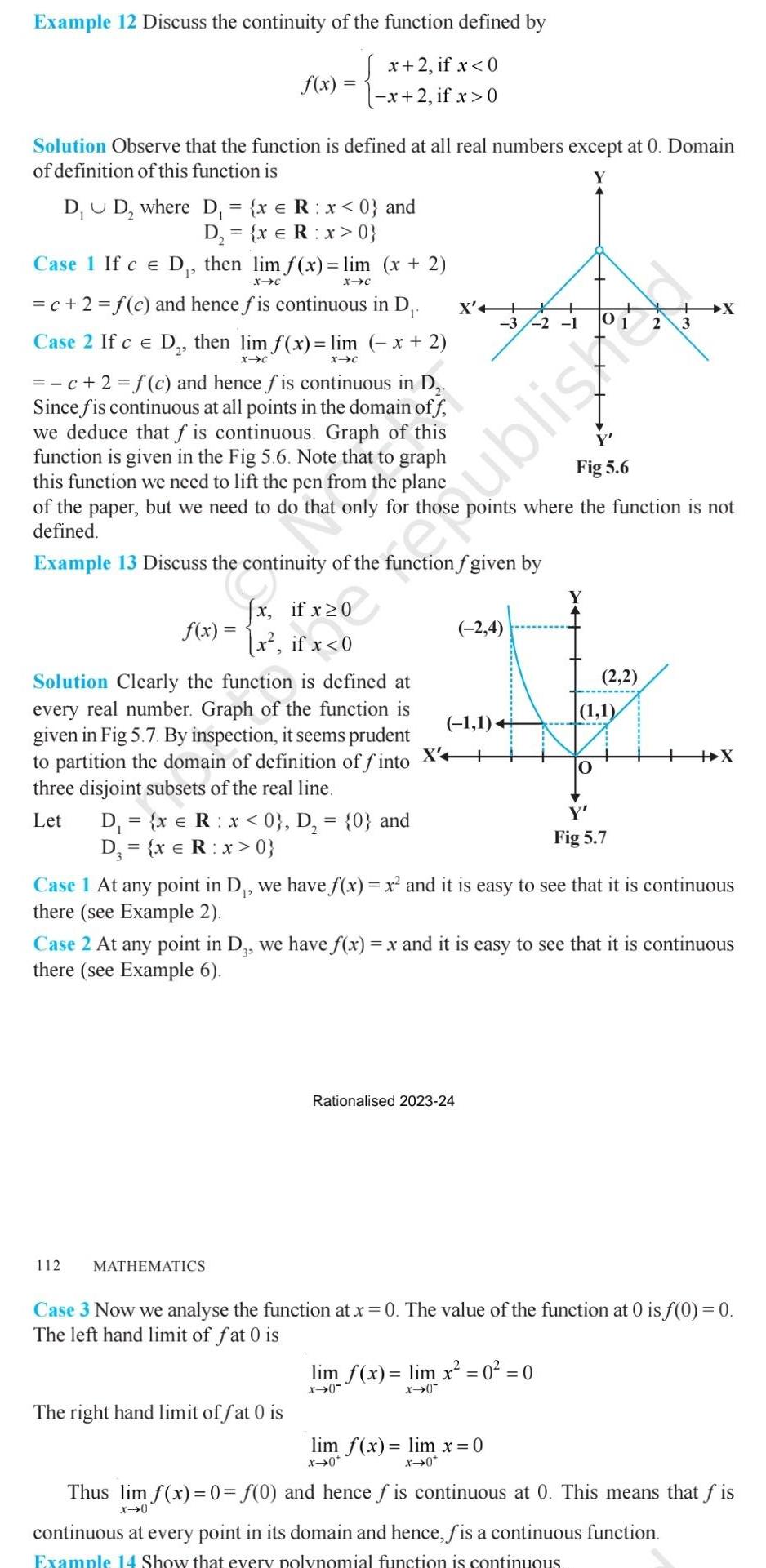
Example 12 Discuss the continuity of the function defined by x+2, if x 0 Solution Observe that the function is defined at all real numbers except at 0. Domain of definition of this function is D D where D = {x = Rx 0} Case 1 If c = D, then lim f(x) = lim (x+2) xc XC =c+2=f(c) and hence f is continuous in D. Case 2 If c = D, then lim f(x) = lim (-x+2) x-c xc 2 X'+ X -3 -2 -1 ublish =c+2=f(c) and hence fis continuous in D, Since fis continuous at all points in the domain of f we deduce that f is continuous. Graph of this function is given in the Fig 5.6. Note that to graph this function we need to lift the pen from the plane Fig 5.6 of the paper, but we need to do that only for thos points where the function is not defined. Example 13 Discuss the continuity of the function f given by (x, if x0 f(x)= x, if x 0} X'4 (-2,4) (2,2) (1,1) (-1,1) O Fig 5.7 X+++ Case 1 At any point in D, we have f(x) = x and it is easy to see that it is continuous there (see Example 2). Case 2 At any point in D3, we have f(x) = x and it is easy to see that it is continuous there (see Example 6). 112 MATHEMATICS Rationalised 2023-24 Case 3 Now we analyse the function at x = 0. The value of the function at 0 is f(0) = 0. The left hand limit of fat 0 is lim f(x)= lim x = 0 = 0 x0" x-0 The right hand limit of fat 0 is lim f(x)= lim x=0 x0* x0* Thus lim f(x)=0= f(0) and hence f is continuous at 0. This means that fis x0 continuous at every point in its domain and hence, fis a continuous function. Example 14 Show that every polynomial function is continuous