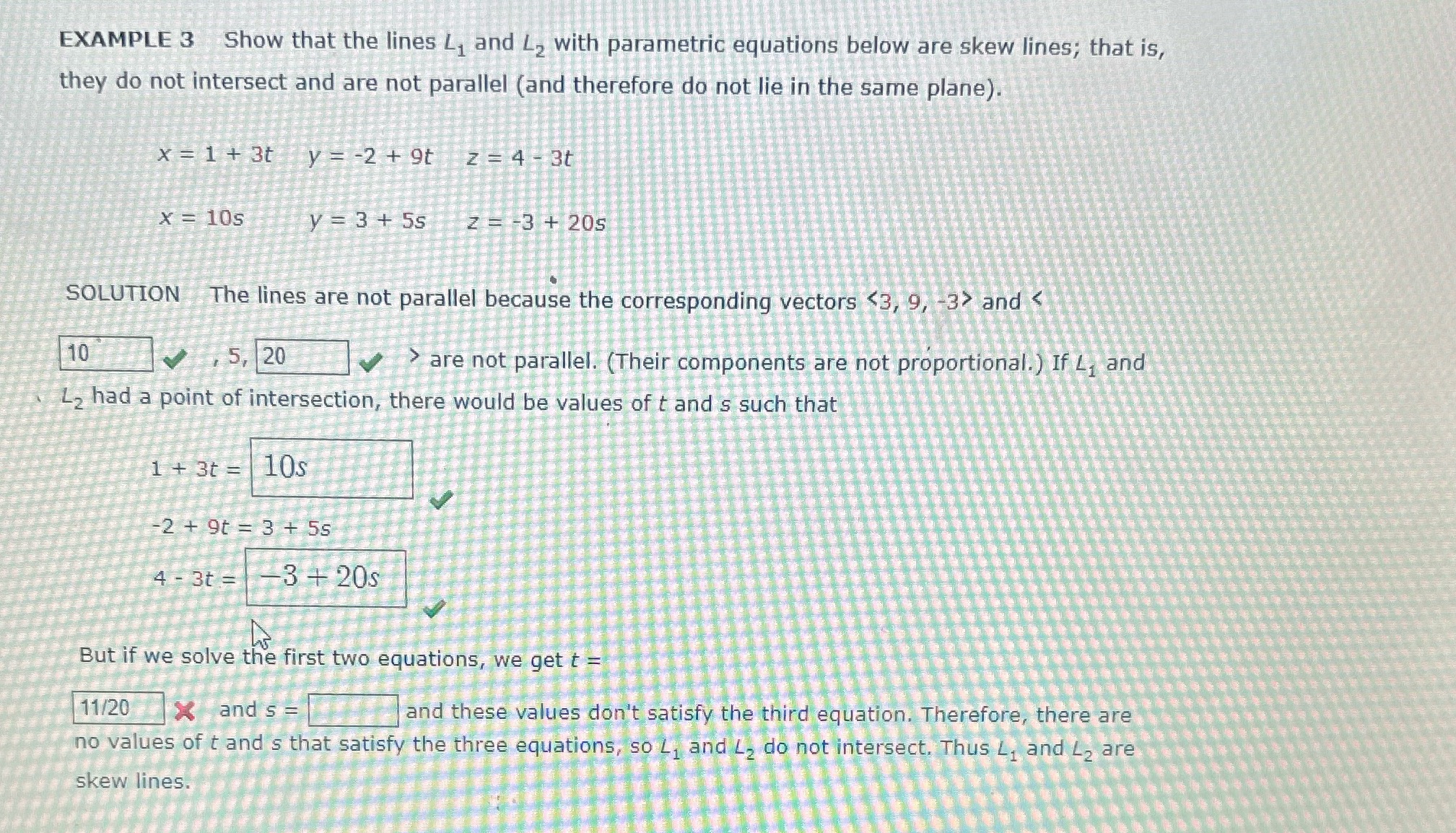
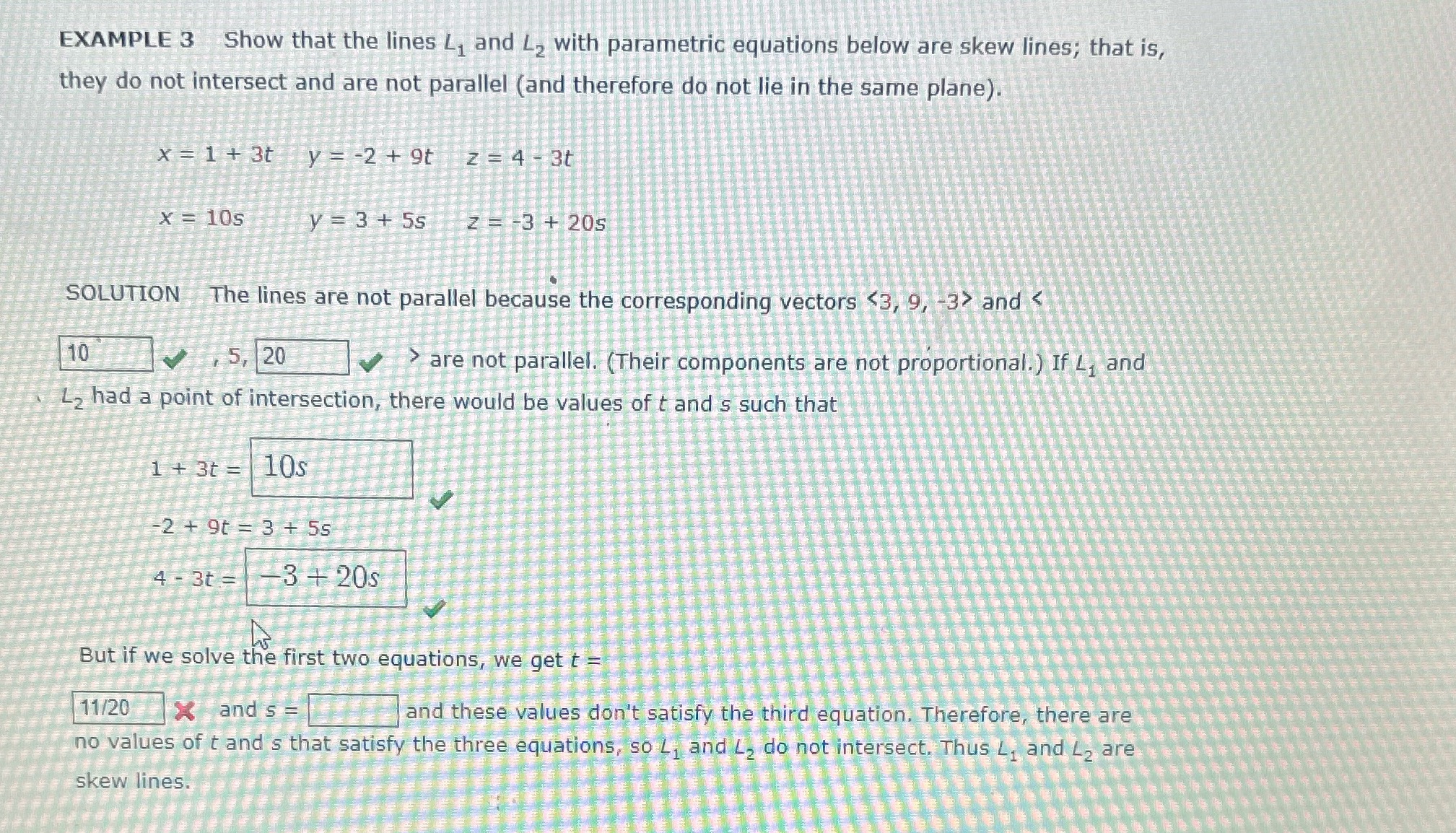
EXAMPLE 3 Show that the lines , and L2 with parametric equations below are skew lines; that is, they do not intersect and are not parallel (and therefore do not lie in the same plane). x = 1 + 3t y = -2 + 9t z =4- 3t X = 10s y = 3 + 5s Z= =3 + 20s SOLUTION The lines are not parallel because the corresponding vectors and are not parallel. (Their components are not proportional. ) If 4, and Ly had a point of intersection, there would be values of t and s such that 1 + 3t = 10s 2 + 9t = 3 + 5s 4 - 3t = -3 + 20s But if we solve the first two equations, we get t = 11/20 X and s = and these values don't satisfy the third equation. Therefore, there are no values of t and's that satisfy the three equations, so L, and 4, do not intersect. Thus Z, and 42 are skew lines