Example 3.3 below

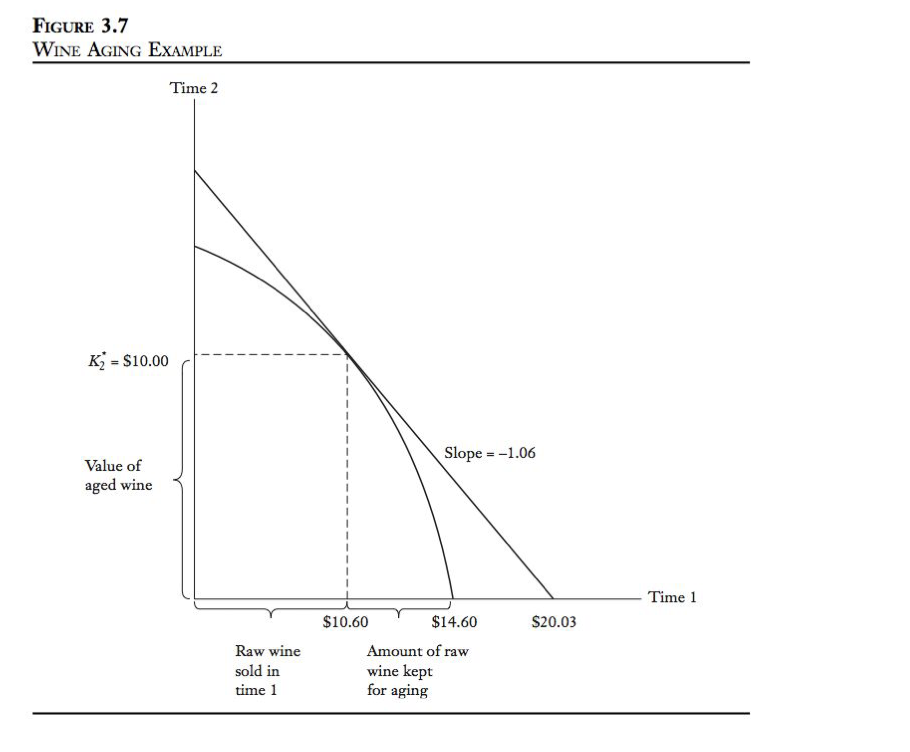
Consider the example in Section 3.3 (wine aging problem) of the Financial Economics textbook but now assume that the marker rate of interest is 10%. Graphically show the operating plan for the following transformation curve: 3K1+2K2=30. 5.3 EXAMPLE: AGING WINE In this section we present a mathematical example as supporting detail for the graphical reasoning presented above. Consider the problem of a businessperson trying to decide whether to sell a product now or refine it further and sell it later at a higher price. For example, assume a vintner who is trying to maximize the market of initially available resources in the form of new wine either by selling the current vintage of wine at time 1 or aging it for sale at time 2. Let the market rate of interest be 6%. The objective function of the vintner will be: maxK1+1.06K2 where K1= value of new wine sold at time 1 K2= value of aged wine sold at time 2 Assume the maximization is subject to K12+K22=212.36, a transformation curve chosen for its mathematical tractability rather than for its interpretive realism. The transformation curve implies that the time 1 cash value of all the raw wine is ($212.36)1/2, or approximately $14.60. Proceeding by substitution, we can rewrite equation (3.4) as: maxK2(212.36K22)1/2+1.06K2 Taking the derivative of equation (3.5) with respect to K2 and setting the result equal to zero, we obtain: (212.36K22)1/221(2K2)+1.061=0 This step is equivalent to saying "choose a production plan such that the marginal rate of return equals the market rate of interest." Rewriting equation (3.6), we obtain the following sequence of calculations: 1.061K2(1.06)K22(1.06)2K22[1+(1.06)2]K22($2.1236)K2=(212.36K22)1/2K2=(212.36K22)1/2=$212.36K22=$212.36=$212.36=$10.00 therefore K1=($212.36$100.00)1/2=$10.60 and MV1=$10.60+1.0610.00=$20.03 This situation is shown graphically in Figure 3.7. Note the following: (1) The vintner has increased initial wealth (MV1) to $20.03 from the original $14.60 available by selling all the raw wine at time 1 ; (2) the vintner will employ wine in the aging process up to the point where the marginal rate of return on aging wine just equals the market rate of interest. FIGURE 3.7 Consider the example in Section 3.3 (wine aging problem) of the Financial Economics textbook but now assume that the marker rate of interest is 10%. Graphically show the operating plan for the following transformation curve: 3K1+2K2=30. 5.3 EXAMPLE: AGING WINE In this section we present a mathematical example as supporting detail for the graphical reasoning presented above. Consider the problem of a businessperson trying to decide whether to sell a product now or refine it further and sell it later at a higher price. For example, assume a vintner who is trying to maximize the market of initially available resources in the form of new wine either by selling the current vintage of wine at time 1 or aging it for sale at time 2. Let the market rate of interest be 6%. The objective function of the vintner will be: maxK1+1.06K2 where K1= value of new wine sold at time 1 K2= value of aged wine sold at time 2 Assume the maximization is subject to K12+K22=212.36, a transformation curve chosen for its mathematical tractability rather than for its interpretive realism. The transformation curve implies that the time 1 cash value of all the raw wine is ($212.36)1/2, or approximately $14.60. Proceeding by substitution, we can rewrite equation (3.4) as: maxK2(212.36K22)1/2+1.06K2 Taking the derivative of equation (3.5) with respect to K2 and setting the result equal to zero, we obtain: (212.36K22)1/221(2K2)+1.061=0 This step is equivalent to saying "choose a production plan such that the marginal rate of return equals the market rate of interest." Rewriting equation (3.6), we obtain the following sequence of calculations: 1.061K2(1.06)K22(1.06)2K22[1+(1.06)2]K22($2.1236)K2=(212.36K22)1/2K2=(212.36K22)1/2=$212.36K22=$212.36=$212.36=$10.00 therefore K1=($212.36$100.00)1/2=$10.60 and MV1=$10.60+1.0610.00=$20.03 This situation is shown graphically in Figure 3.7. Note the following: (1) The vintner has increased initial wealth (MV1) to $20.03 from the original $14.60 available by selling all the raw wine at time 1 ; (2) the vintner will employ wine in the aging process up to the point where the marginal rate of return on aging wine just equals the market rate of interest. FIGURE 3.7