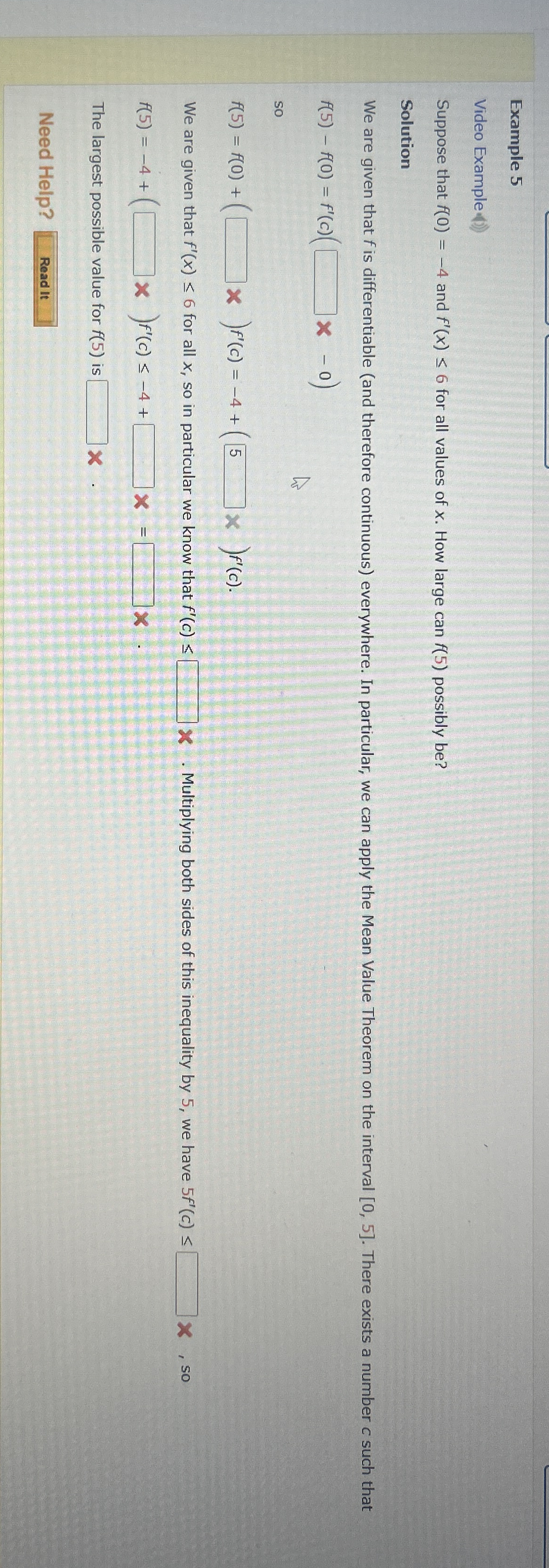
Example $5$

Video Example

Suppose that $f(0)=-4$ and $f^{\text{'}}(x)6$ for all values of $x.$ How large can $f(5)$ possibly be$?$

Solution

We are given that $f$ is differentiable $($and therefore continuous$)$ everywhere. In particular, we can apply the Mean Value Theorem on the interval $[0,5].$ There exists a number $c$ such that $f(5)-f(0)=f^{\text{'}}(c)(x-0)$

so

$f(5)=f(0)+(,x)f^{\text{'}}(c)=-4+(,x)f^{\text{'}}(c)$

We are given that $f^{\text{'}}(x)6$ for all $x,$ so in particular we know that $f^{\text{'}}(c)$ X $.$ Multiplying both sides of this inequality by $5,$ we have $5f^{\text{'}}(c),$ so

$(x|)-4+,x=$

The largest possible value for $f(5)$ is $$