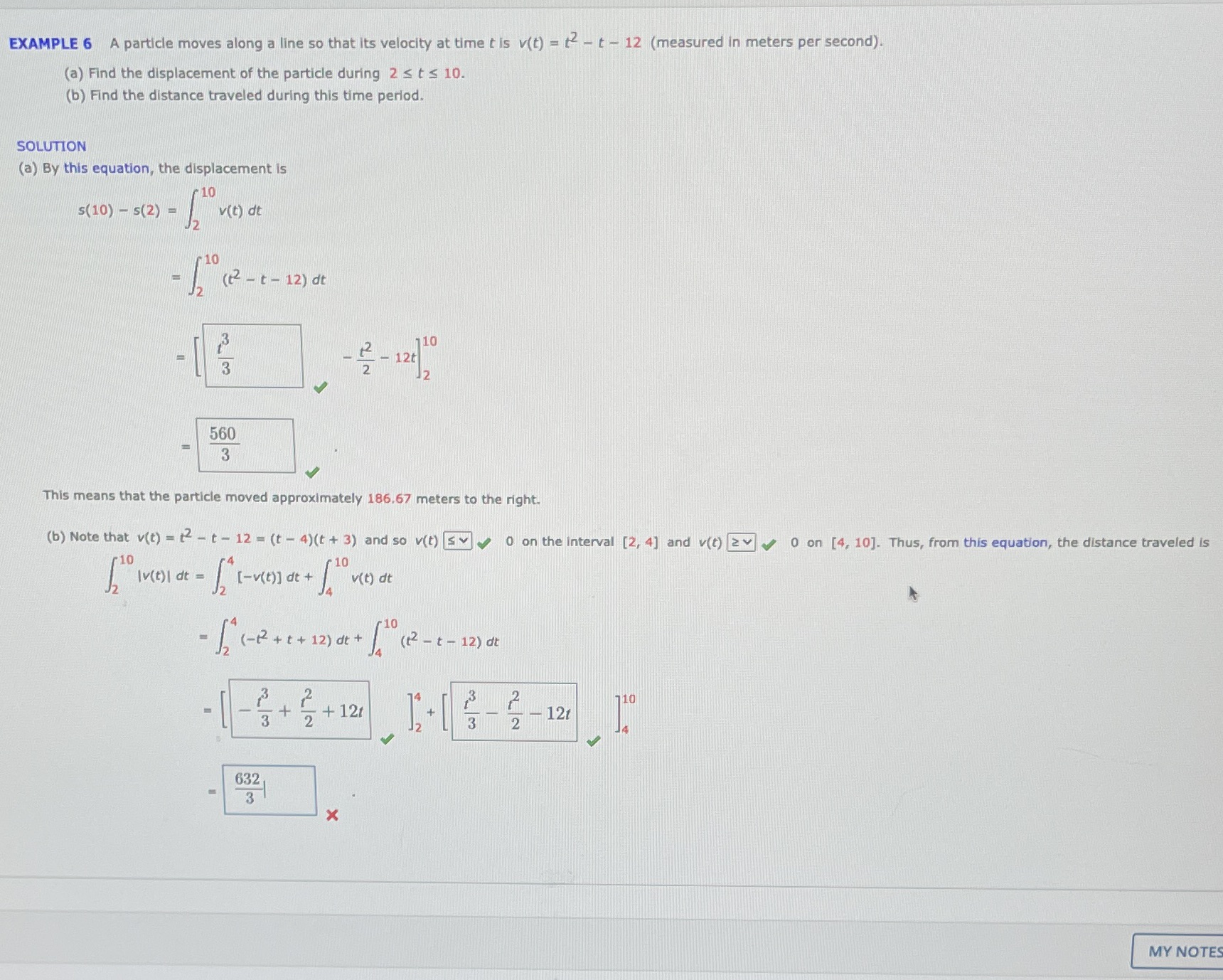
EXAMPLE 6 A particle moves along a line so that its velocity at time t is v(t) = t - t - 12 (measured in meters per second). (a) Find the displacement of the particle during 2 s t s 10. (b) Find the distance traveled during this time period. SOLUTION (a) By this equation, the displacement is s(10) - s(2) - v(t) dt (2 - t - 12) at - 12t 560 3 This means that the particle moved approximately 186.67 meters to the right. (b) Note that v(t) = 12 - t - 12 = (t - 4)(t + 3) and so v(t) [s v v o on the interval [2, 4] and v(t) 2 v w/ 0 on [4, 10]. Thus, from this equation, the distance traveled is -12 ( - 2 + 1 + 12 ) at + / ( 2 - 1 - 12 ) dt 1 - 8 +2 +1 2 - 12t 632 3 X MY NOTES