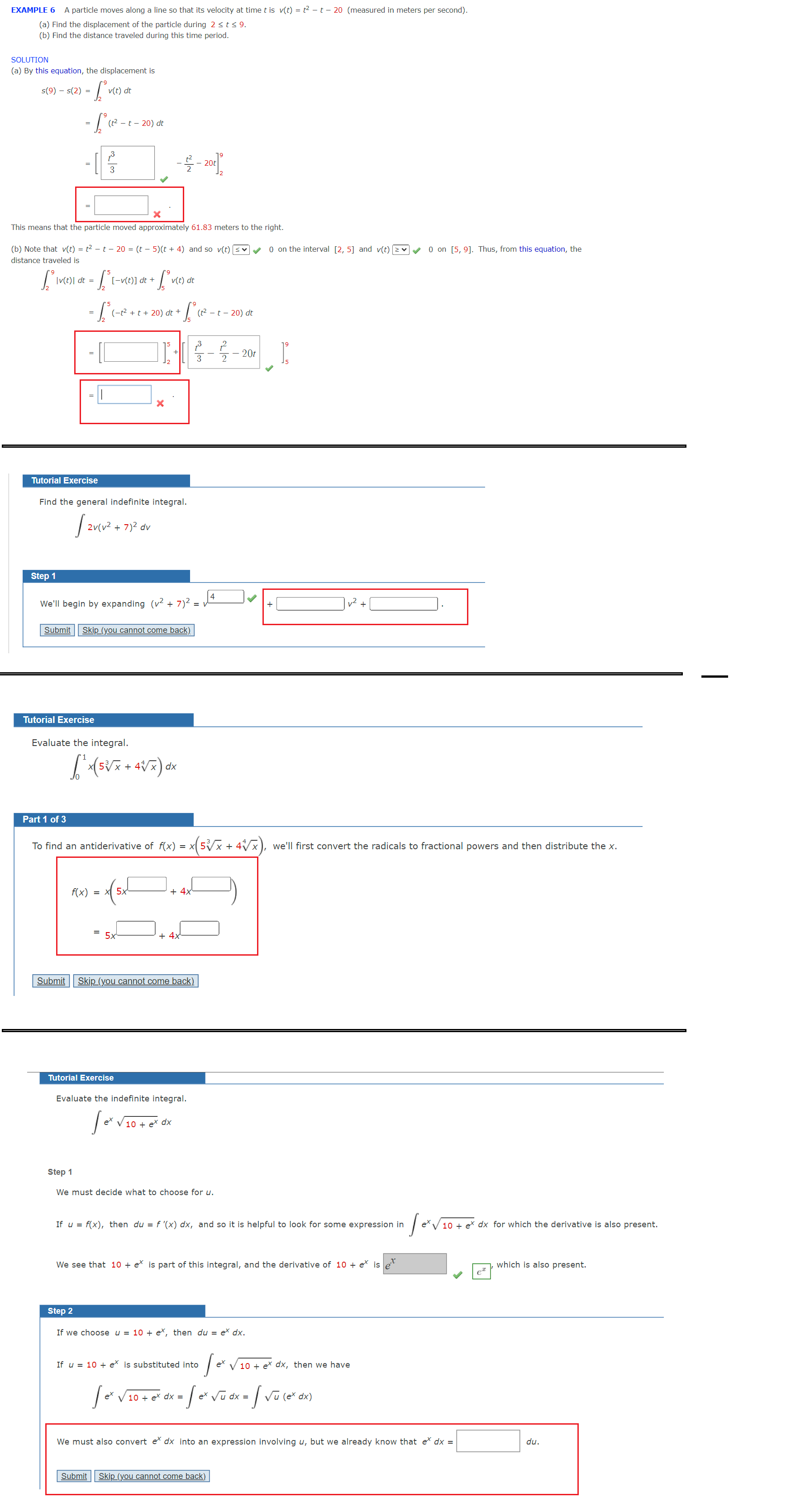
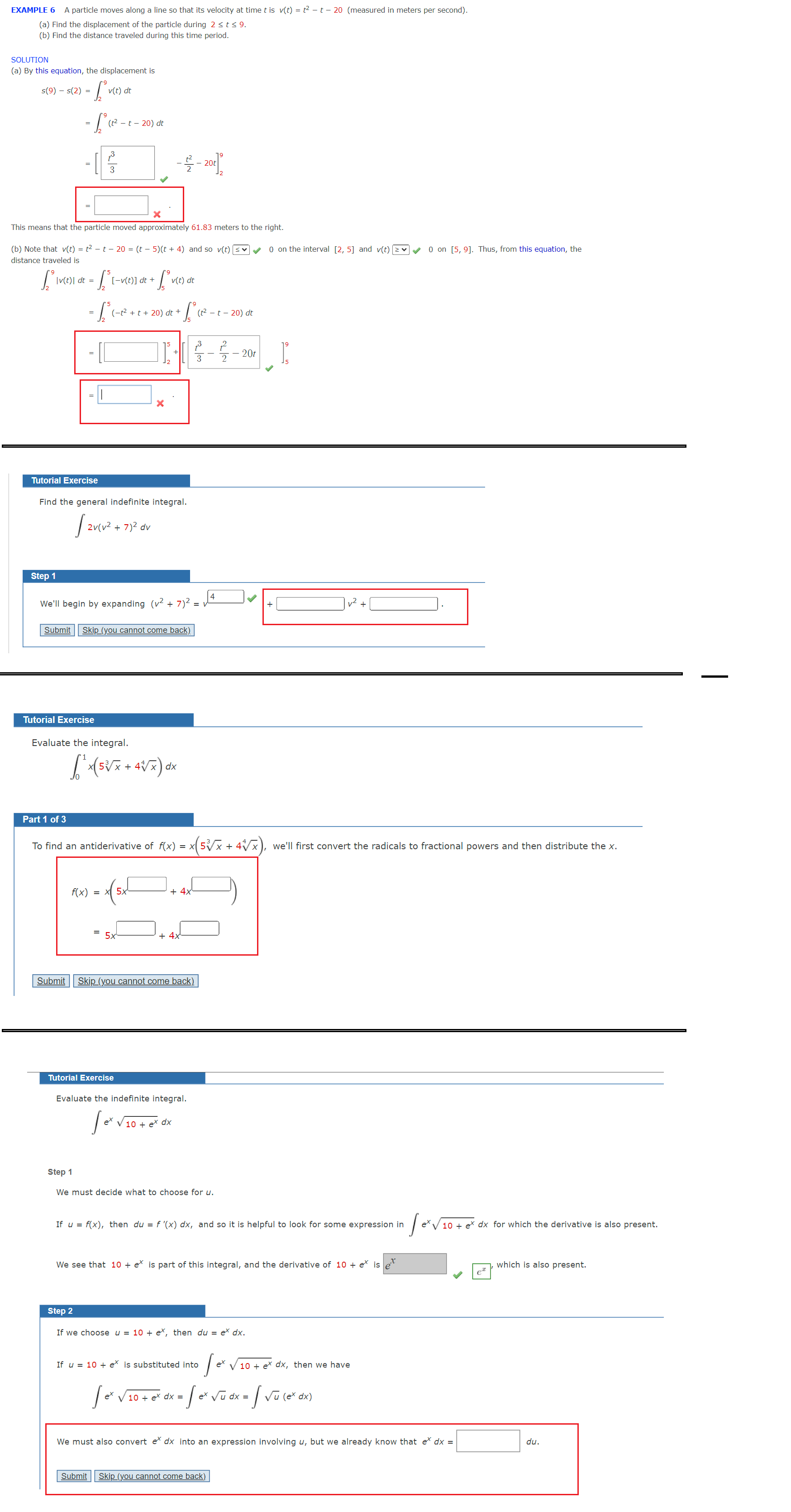
EXAMPLE 6 A particle moves along a line so that its velocity at time t is v(t) = t2 - t - 20 (measured in meters per second). (a) Find the displacement of the particle during 2 S t s 9. (b) Find the distance traveled during this time period. SOLUTION (a) By this equation, the displacement is 5 (9) - 5( 2 ) = v ( t ) at (2 -t-20) dt 42 - 20t This means that the particle moved approximately 61.83 meters to the right. (b) Note that v(t) = 12 - t - 20 = (t - 5)(t + 4) and so v(t) [sv . 0 on the interval [2, 5] and v(t) [zy . 0 on [5, 9]. Thus, from this equation, the distance traveled is 12 ( - 2 + + + 20 ) at + / ( 12 - 1 - 20 ) dt 2 - 20t Tutorial Exercise Find the general indefinite integral. 2V ( v 2 + 7 ) 2 dv Step 1 We'll begin by expanding (v2 + 7) 2 = / 4 -. Submit Skip (you cannot come back). Tutorial Exercise Evaluate the integral. Part 1 of 3 To find an antiderivative of f(x) = x(5Vx + 4\\x ), we'll first convert the radicals to fractional powers and then distribute the x. F( X ) = x 5x + 4x = 5X Submit Skip (you cannot come back) Tutorial Exercise Evaluate the indefinite integral. ex viot ex dx Step 1 We must decide what to choose for u. If u = f(x), then du = f '(x) dx, and so it is helpful to look for some expression in exv 10 + ex dx for which the derivative is also present. We see that 10 + ex is part of this integral, and the derivative of 10 + ex is et ex which is also present. Step 2 If we choose u = 10 + ex, then du = ex dx. If u = 10 + ex is substituted into ex v 10 + ex dx, then we have fe viotexax = ( ex vuax = / Vu(ex dx ) We must also convert edx into an expression involving u, but we already know that ex dx = du . Submit Skip (you cannot come back)