Question: Example 7.46: Consider the linear dynamical system VA+1 = AV, with A=[3 _1], and Vo = ] To find a formula for Vic, we first

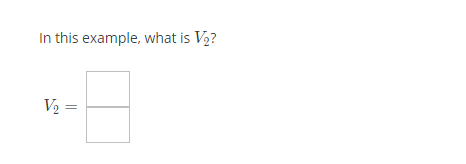
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


